Jfyhkgu

経緯度（けいいど、longitude and latitude）とは経度（longitude）および緯度（latitude）を指し、地球（および天体）表面上で位置（点）を示すための座標表現である。本稿では地理座標系で用いられる経緯度を説明する。

基本的に、その天体の表面点の垂直ベクトルを考え、その向きを球面座標で表現する^[1]。

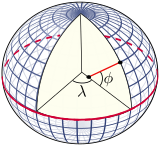
経度（λ{displaystyle lambda }）、緯度（ϕ{displaystyle phi }）、および垂直線（赤）。

ECEF直交座標・地理座標・局所座標の関係（回転楕円体面上）。(X,Y,Z){displaystyle (X,Y,Z)}および方位角θ{displaystyle theta }の取り方は右手系。

地理経緯度と天文経緯度

経緯度は基本的にその地表点の垂直ベクトルに基づき、そのベクトルの方向を数値化したものである。
すなわち｛経度λ{displaystyle lambda }、緯度ϕ{displaystyle phi }｝⇔｛局所垂直ベクトル(cos⁡ϕcos⁡λ,cos⁡ϕsin⁡λ,sin⁡ϕ){displaystyle (cos phi cos lambda ,,cos phi sin lambda ,,sin phi )}｝。

地理座標系で用いられる地理経緯度（geographic longitude and latitude）^[2]は、地球を回転楕円体と見なし、その面の法線ベクトル方向に基づく。

ただし歴史的には、地表の鉛直線に基づく垂直方向（天頂）が天球のどこを指すかによって決めた天文経緯度（astronomical longitude and latitude）が使われてきた。これは地球の重力の鉛直線偏差の影響（加えて地球の極運動の影響）を被っている。従って、距離・面積との関係も簡素にならない。

地理学・測地学の発展とともに、経緯度原点を国内に設け、その地点の天文経緯度を原点として位置づけ、接する準拠楕円体に基づく地理経緯度を用いる方式が行われた（地域的測地系）。

地理経緯度の変換式

地理座標（経度λ{displaystyle lambda }、緯度ϕ{displaystyle phi }、高度（楕円体高）h{displaystyle h}）とECEF直交座標系(x,y,z){displaystyle (x,y,z)}との変換、および微小量の式は下記となる（地球楕円体の長半径a{displaystyle a}、離心率e=f(2−f){displaystyle e={sqrt {f(2-f)}}}）。

{x=(N(ϕ)+h)cos⁡ϕcos⁡λ,y=(N(ϕ)+h)cos⁡ϕsin⁡λ,z=(N(ϕ)(1−e2)+h)sin⁡ϕ,{displaystyle {begin{cases}x=left(N(phi )+hright)cos {phi }cos {lambda },\y=left(N(phi )+hright)cos {phi }sin {lambda },\z=left(N(phi )(1-e^{2})+hright)sin {phi },end{cases}}}

(dxdydz)=(−sin⁡λ−sin⁡ϕcos⁡λcos⁡ϕcos⁡λcos⁡λ−sin⁡ϕsin⁡λcos⁡ϕsin⁡λ0cos⁡ϕsin⁡ϕ)(dEdNdU),(dEdNdU)=((N(ϕ)+h)cos⁡ϕ000M(ϕ)+h0001)(dλdϕdh),N(ϕ)≜a1−e2sin2⁡ϕ,M(ϕ)≜a(1−e2)(1−e2sin2⁡ϕ)3/2.{displaystyle {begin{aligned}{begin{pmatrix}dx\dy\dz\end{pmatrix}}&={begin{pmatrix}-sin lambda &-sin phi cos lambda &cos phi cos lambda \cos lambda &-sin phi sin lambda &cos phi sin lambda \0&cos phi &sin phi \end{pmatrix}}{begin{pmatrix}dE\dN\dU\end{pmatrix}},\{begin{pmatrix}dE\dN\dU\end{pmatrix}}&={begin{pmatrix}left(N(phi )+hright)cos phi &0&0\0&M(phi )+h&0\0&0&1\end{pmatrix}}{begin{pmatrix}dlambda \dphi \dh\end{pmatrix}},\N(phi )&triangleq {frac {a}{sqrt {1-e^{2}sin ^{2}phi }}},\M(phi )&triangleq {frac {a(1-e^{2})}{left(1-e^{2}sin ^{2}phi right)^{3/2}}}.end{aligned}}}

微小量三成分はどれも互いに直交方向となる。h=0{displaystyle h=0}では回転楕円体となり、また子午線弧（経線弧）の曲率半径はM(ϕ){displaystyle M(phi )}、卯酉線弧はN(ϕ){displaystyle N(phi )}（緯線弧はN(ϕ)cos⁡ϕ{displaystyle N(phi )cos phi }）^[3]となる。

(x,y,z){displaystyle (x,y,z)}から(λ,ϕ,h){displaystyle (lambda ,,phi ,,h)}を求める変換計算については上記から導かれる ϕ{displaystyle phi } の方程式を解く必要がある^[4]。

経度・緯度を並べる順序

並べる順序には、異なる慣行が存在する。正負については、東経を正の経度λ{displaystyle lambda }、北緯を正の緯度ϕ{displaystyle phi }、南緯向きを正の余緯度とする。

• 
  右手系では：（経度、緯度、及び高度）の順とする^[5][6]。


• これに対して左手系^[7]では：（緯度、経度、及び高度）の順とする。局所座標系（地平面）の x{displaystyle x} 方向が北・緯度座標、y{displaystyle y} 方向が東・経度座標となる。

地図投影法の表式における x, y{displaystyle x, y} 平面座標の取り方

地図学における地図投影法の表式で x, y{displaystyle x, y} 平面座標の取り方は右手系で表されることが多い。

• 
  右手系：x{displaystyle x}方向を右横方向、y{displaystyle y}方向を上縦方向


• 
  左手系：x{displaystyle x}方向を上縦方向、y{displaystyle y}方向を右横方向^[8][9]
  

方位角との対応関係

方位角は上記と対応した関係が存在する：

• 
  右手系（反時計回り）：（東→北→西→南）^[10]
  


• 
  左手系^[7]（時計回り）：（北→東→南→西）

方位角を θ{displaystyle theta }として、局所座標系（地平面）の単位円は (x,y,z)=(cos⁡θ,sin⁡θ,0){displaystyle (x,y,z)=(cos theta ,sin theta ,0)} となる。

右手系経緯度の採用

下記では右手系経緯度が採用されている。

• OpenLayers


• MapboxGL


• KML


• GeoJSON


• Well-known text


• MySQL


• MongoDB


• Redis


• Oracle Spatial


• Solr


• Elasticsearch


• Geocouch


• OSRM

polygonの頂点配列が時計周り順

右手系経緯度を採用しているもののうち、polygonの頂点配列順については時計周り順（左手系）を採用しているものがある：

• Shapefile


• 
  ArcGIS API for JavaScript


• D3.js


• PostGIS


• SpatiaLite


• TopoJSON

左手系経緯度の採用

下記では左手系経緯度（緯度、経度の順）が採用されている。

• Leaflet


• 
  Google Maps API


• Apple MapKit
  


• ArangoDB


• GeoRSS


• 
  Open Geospatial Consortium (OGC)の Spatial Reference System (SRS)^[11]
  

左手系地図投影法の採用

下記では左手系の地図投影法を採用し、平面座標のx{displaystyle x}軸は右横方向が正、y{displaystyle y}軸は下縦方向が正としている^[12]。

• Mapbox Vector Tiles

関連項目

• 経緯線


• 日本経緯度原点


• IERS基準子午線


• 地理座標系


• メルカトル図法


• 
  平面直角座標系（日本の規格。左手系）


• 
  ISO 6709 (座標の文字列表現の国際標準。原則として左手系）

脚注

1. 
   ^ 天体が球体であれば、球面上の垂直ベクトルは中心を通るので、地理経緯度は地心経緯度に等しい。
   


2. 
   ^ 地理経緯度は測地経緯度、測地学的経緯度（geodetic longitude and latitude）とも呼ばれる。
   


3. 
   ^ ムーニエの定理も参照。
   


4. 
   ^ 解くべき ϕ{displaystyle phi } の方程式は
   

   pcos⁡ϕ−zsin⁡ϕ−e2N(ϕ)=0,p=x2+y2{displaystyle {begin{aligned}&{frac {p}{cos phi }}-{frac {z}{sin phi }}-e^{2}N(phi )=0,\&p={sqrt {x^{2}+y^{2}}}end{aligned}}}

   
   で、またこれは変数 κ=pztan⁡ϕ{displaystyle kappa ={frac {p}{z}}tan phi }についての方程式に帰着できる：
   

   κ−1−e2aκp2+(1−e2)z2κ2=0{displaystyle kappa -1-{frac {e^{2}akappa }{sqrt {p^{2}+(1-e^{2})z^{2}kappa ^{2}}}}=0}

   
   解き方はGeodetic system#Conversion calculations等を参照のこと。またh=e−2(κ−1−(1−e2))p2+z2κ2{displaystyle h=e^{-2}(kappa ^{-1}-(1-e^{2})){sqrt {p^{2}+z^{2}kappa ^{2}}}}
   


5. 
   ^ 和漢の用例でも、この（経度・緯度）の順である「経緯度」である（例えば「日本経緯度原点」、「経緯線」）。
   


6. 
   ^ 右手系の別慣行の変数及び順序は：（余緯度、経度、及び高度）。数学・物理学における球面座標系の標準はこれに当たる。
   


7. ^ ^abこの左手系の使用は一般的には非推奨とされている。ただし測量、航海術や地理学などの分野はこの左手系の使用は極めて標準的である。
   


8. 
   ^ 左手系の別慣行では、x{displaystyle x}方向を右横方向、y{displaystyle y}方向を下縦方向にとる。
   


9. 
   ^ 平面直角座標系（日本の規格）では左手系である。
   


10. 
    ^ 右手系の別慣行では：（南→東→北→西）
    


11. 
    ^ OGCによるSRS/CRS の定義では大多数の測地系は axis order を左手系経緯度と定義する。
    


12. 
    ^ 他にSVGフォーマットでは左手系座標が採用されている。
    

この項目は、地理用語に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（Portal:地理学）。