Radiazione cosmica di fondo
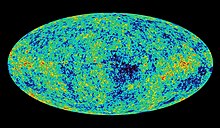
Mappa della radiazione cosmica di fondo, dopo la rimozione dei contributi dovuti a sorgenti locali e dell'anisotropia di dipolo.
In cosmologia la radiazione cosmica di fondo, detta anche radiazione di fondo, abbreviata in CMBR (dall'inglese Cosmic Microwave Background Radiation), è la radiazione elettromagnetica che permea l'universo, considerata come prova del modello del Big Bang[1].
Nonostante lo spazio tra stelle e galassie appaia nero con un telescopio ottico tradizionale, tramite un radiotelescopio è possibile rilevare una debole radiazione isotropa che non è associata ad alcuna stella, galassia o altro corpo celeste e che ha intensità maggiore nella regione delle microonde dello spettro elettromagnetico.
La CMBR venne scoperta nel 1964 dagli astronomi statunitensi Arno Penzias e Robert Woodrow Wilson[2] al termine di uno studio avviato nel 1940, che li portò a conseguire il Premio Nobel per la fisica nel 1978.
Indice
1 Introduzione
2 Caratteristiche
3 Scoperta
4 Relazioni con il Big Bang
4.1 Temperatura
4.2 Spettro di potenza
5 Anisotropie della CMB
5.1 Anisotropie primarie
5.2 Anisotropie secondarie
5.3 Anisotropia di dipolo
5.4 Polarizzazione
6 Osservazioni della radiazione di fondo
7 Riduzione e analisi dei dati
7.1 Anisotropie di dipolo
7.2 Multipoli a basso valore di «l» ed altre anomalie
8 Note
9 Altri progetti
10 Collegamenti esterni
Introduzione |

Mappatura completa delle fluttuazioni della temperatura nello spazio, ripresa dal WMAP nel 2003.
La radiazione di fondo è definibile come la radiazione residua proveniente dalle fasi iniziali della nascita dell'universo in accordo con il modello del Big Bang, di cui è considerata una conferma chiave.
Nelle fasi iniziali della vita, prima della formazione di stelle e pianeti, l'universo aveva dimensioni molto più contenute di quelle attuali, era molto più caldo e permeato da una radiazione uniforme in stretta interazione con il plasma di idrogeno. L'elevata energia dei fotoni impediva agli elettroni di legarsi ai protoni, impedendo la formazione degli atomi. Con l'espansione dell'universo, sia il plasma che la radiazione iniziarono a raffreddarsi, fino a raggiungere una temperatura a cui la minor energia dei fotoni non era più in grado di impedire la formazione dei primi atomi stabili. Questi non poterono più assorbire la radiazione termica, cosicché l'universo, che fino a quel momento era stato una sorta di nebbia opaca, diventò trasparente alla radiazione. I fotoni che esistevano in quel momento iniziarono a propagarsi, divenendo meno energetici, dal momento che andavano a riempire un universo più grande.
Misure precise della radiazione cosmica di fondo sono fondamentali per la cosmologia, dal momento che qualsiasi modello proposto dell'universo deve essere in grado di spiegare questa radiazione. La CMB ha uno spettro termico di corpo nero ad una temperatura di 2,725 K, quindi lo spettro presenta dei picchi nella zona delle microonde alla frequenza di 160,2 GHz, corrispondenti ad una lunghezza d'onda di 1,9 millimetri[3]. L'emissione è quasi, ma non del tutto, uniforme in tutte le direzioni, e mostra un andamento molto specifico corrispondente a quello che si otterrebbe da un gas molto caldo e quasi uniforme che si espandesse fino alle attuali dimensioni dell'universo. In particolare, la distribuzione spaziale dell'energia dello spettro (cioè la differenza osservata in funzione della distanza delle regioni del cielo) contiene piccole anisotropie, o irregolarità, che variano con la dimensione della regione in esame. Queste anisotropie sono state misurate in dettaglio, e corrispondono a quanto ci si aspetterebbe se piccole oscillazioni termiche, generate da fluttuazioni quantistiche della materia in uno spazio ristretto, si fossero espanse fino alla dimensione dello spazio attualmente osservabile. Questo è ancora un settore molto attivo di studio, con gli scienziati che cercano sia dati più accurati (per esempio con la sonda Planck) sia una migliore interpretazione delle condizioni iniziali di espansione.
Anche se molti processi differenti possono produrre la forma generale di uno spettro di corpo nero, nessun modello diverso dal Big Bang ha finora spiegato le fluttuazioni. Per questo la maggior parte dei cosmologi ritiene che il modello del Big Bang sia quello che dà la miglior interpretazione della radiazione di fondo.
Caratteristiche |

Lo spettro della radiazione di fondo misurato dal COBE è la misurazione più precisa di corpo nero in natura[4]. La curva teorica si sovrappone pressoché esattamente ai punti dei dati reali comprensivi delle barre di errore standard.
La radiazione cosmica di fondo è isotropa fino a circa una parte su 100.000: infatti il valore quadratico medio delle variazioni è di solo 18 µK.[5][6]. Lo spettrofotometro FIRAS (Far-Infrared Absolute Spectrophotometer) montato sul COBE della NASA, ha accuratamente misurato il suo spettro. I membri del progetto FIRAS hanno confrontato la CMB con la radiazione di corpo nero del riferimento interno dello strumento, e hanno trovato che gli spettri corrispondono entro l'errore sperimentale. Hanno concluso che qualsiasi deviazione dalla forma del corpo nero che potrebbe ancora non essere stata individuata nello spettro della CMB nella gamma di lunghezze d'onda 0,5–5 mm, deve avere un valore quadratico medio ponderato al massimo di 50 parti per milione (0,005%) rispetto al picco di luminosità della CMB[7]. Questo ha reso lo spettro della CMB lo spettro di corpo nero misurato con più precisione in natura[4].
La radiazione cosmica di fondo è forse la previsione principale del modello del Big Bang. Inoltre, la cosmologia inflazionaria prevede che dopo circa 10−37 secondi[8], l'universo appena nato abbia subito una crescita esponenziale che appianò quasi tutte le disomogeneità.[9][10] A questo seguì la rottura spontanea di simmetria, un tipo di transizione di fase che ha fissato le interazioni fondamentali e le particelle elementari nella loro forma attuale. Dopo 10−6 secondi, l'universo primordiale era costituito da un plasma caldissimo di fotoni, elettroni, e barioni. I fotoni interagivano continuamente con il plasma attraverso lo scattering Thomson. L'espansione dell'universo, con il conseguente raffreddamento adiabatico, ha causato il raffreddamento del plasma fino a rendere possibile la combinazione degli elettroni con i protoni, per dare così luogo agli atomi di idrogeno. Questo evento di ricombinazione è avvenuto quando la temperatura era scesa a circa 3000 K, cioè quando l'età dell'universo era di circa 379 000 anni[11][12]. A questo punto, i fotoni hanno potuto allontanarsi dagli atomi ora elettricamente neutri e hanno iniziato a viaggiare liberamente nello spazio, con il conseguente disaccoppiamento tra la materia e la radiazione[13].
Da allora la temperatura di colore dei fotoni ha continuato a diminuire; attualmente ha raggiunto i 2,725 K, e continua a scendere mentre l'universo si espande. Secondo il modello del Big Bang, la radiazione che misuriamo oggi nel cielo proviene da una superficie sferica chiamata superficie di ultimo scattering. Questo rappresenta l'insieme dei punti nello spazio in cui si ritiene sia avvenuto l'evento di disaccoppiamento, a meno di 400 000 anni dopo il Big Bang[14]; i fotoni che ci hanno appena raggiunto provengono da questo remoto punto nel tempo. L'età stimata dell'Universo è di 13,75 miliardi di anni[15]. Tuttavia, poiché l'Universo ha continuato ad espandersi da allora, la distanza comovente dalla Terra al bordo dell'universo osservabile è ora di almeno 46,5 miliardi anni luce.[16][17]
La teoria del Big Bang suggerisce che la radiazione cosmica di fondo riempia tutto lo spazio osservabile, e che la maggior parte dell'energia di radiazione nell'universo sia nella radiazione cosmica di fondo[18], che costituisce una frazione di circa 6 × 10−5 della densità totale dell'universo[19].
Due dei più grandi successi della teoria del big bang sono la previsione del suo spettro quasi perfetto di corpo nero e la previsione dettagliata delle anisotropie della radiazione cosmica di fondo. La sonda WMAP ha misurato con precisione queste anisotropie su tutto il cielo fino a scale angolari di 0,2 gradi[20]. Queste possono essere usate per stimare i parametri del modello Lambda-CDM standard del Big Bang. Alcune informazioni, come ad esempio la forma dell'universo, possono essere ottenute direttamente dalla radiazione cosmica di fondo, mentre altre, come la costante di Hubble, non sono collegate e devono essere dedotte da altre misurazioni[20]. Il valore di quest'ultima dà lo spostamento verso il rosso delle galassie (da interpretare come la velocità di recessione) in proporzione alla loro distanza.
Scoperta |
Cronologia della CMB | |
|---|---|
Date e persone fondamentali | |
| 1941 | Andrew McKellar segnala l'osservazione di una temperatura bolometrica media di 2,3 K, basata sullo studio delle righe di assorbimento interstellare[21][22]. |
| 1946 | Robert Dicke predice una "... radiazione di materia cosmica" a ~20 K, ma non si riferisce alla radiazione di fondo.[23] |
| 1948 | George Gamow calcola una temperatura di 50 K (ipotizzando un universo di 3 miliardi di anni di età)[24], commentando che ".. è in accordo ragionevole con la temperatura reale dello spazio interstellare", ma non fa menzione della radiazione di fondo. |
| 1948 | Ralph Alpher e Robert Herman stimano "la temperatura dell'Universo" a 5 K. Anche se non menzionano esplicitamente la radiazione di fondo a microonde, lo si può dedurre[25]. |
| 1950 | Ralph Alpher and Robert Herman ricalcolano la temperatura a 28 K. |
| 1953 | George Gamow stima la temperatura a 7 K[23]. |
| 1955 | Émile Le Roux del Radio Nançay Observatory, in uno studio del cielo a λ = 33 cm, riporta un radiazione di fondo quasi isotropa di 3 ± 2 K[23]. |
| 1956 | George Gamow stima la temperatura a 6 K[23]. |
1957 | Tigran Shmaonov riporta che "la temperatura assoluta effettiva del fondo di emissione radio ... è di 4 ± 3 K".[26] Va osservato che la "misurazione ha mostrato che l'intensità delle radiazioni è indipendente dal tempo e dalla direzione di osservazione ... è ormai chiaro che Shmaonov aveva osservato la radiazione cosmica di fondo alla lunghezza d'onda di 3,2 cm".[27] |
| anni 1960 | Robert Dicke stima nuovamente la temperatura della CMB a 40 K.[23] |
| 1964 | A. G. Doroshkevich e Igor Dmitriyevich Novikov pubblicano una breve nota, dove menzionano la CMB come fenomeno osservabile[28]. |
| 1964–65 | Arno Penzias e Robert Woodrow Wilson misurano una temperatura di circa 3 K. Robert Dicke, James Peebles, P. G. Roll, e David Todd Wilkinson interpretano questa radiazione come una firma del Big Bang. |
| 1978 | Arno Penzias e Robert Woodrow Wilson ricevono il Premio Nobel per la fisica. |
| 1983 | L'Unione Sovietica lancia la sonda RELIKT-1 per lo studio della CMB. |
| 1990 | FIRAS misura la forma del corpo nero dello spettro della CMB con una precisione molto alta. |
| Gennaio 1992 | Gli scienziati che hanno analizzato i dati della RELIKT-1 dichiarano la scoperta delle anisotropie al seminario astrofisico di Mosca[29]. |
| Aprile 1992 | Gli scienziati che hanno analizzato i dati del COBE annunciano la scoperta della temperatura primaria delle anisotropie[30]. |
| 1999 | Prime misurazioni delle oscillazioni acustiche nelle anisotropie angolari dello spettro della CMB, dalle sonde TOCO, BOOMERanG e MAXIMA. |
| 2002 | Polarizzazione scoperta dalla sonda DASI[31]. |
| 2004 | Spettro della polarizzazione E-mode ottenuto dal telescopio CBI[32]. |
| 2005 | Ralph Alpher viene insignito della National Medal of Science per il suo lavoro pionieristico nella nucleosintesi e la previsione che l'espansione dell'universo lascia dietro di sé la radiazione di fondo, fornendo così un modello per la teoria del Big Bang. |
| 2006 | Due dei ricercatori principali del COBE, George Fitzgerald Smoot e John Cromwell Mather, ricevono il Premio Nobel per la fisica per il loro lavoro sulle misure di precisione della CMB. |
La radiazione di fondo venne predetta nel 1948 da George Gamow, Ralph Alpher, e Robert Herman.[33][34][35]
Alpher e Herman sono stati in grado di stimare la temperatura della radiazione cosmica di fondo a 5 K, anche se due anni dopo la ricalcolano a 28 K.[36] Anche se ci sono state diverse stime precedenti della temperatura dello spazio[37], queste soffrivano di due difetti. In primo luogo, erano misure della temperatura effettiva dello spazio e non lasciavano supporre che lo spazio sia stato riempito con uno spettro termico di Planck. Poi, dipendono dalla nostra posizione speciale ai margini della Via Lattea e non specificano che la radiazione è isotropa. Le stime produrrebbero previsioni molto diverse se la Terra si trovasse in un altro punto dell'universo.[38]
I risultati del 1948 di Alpher e Herman vennero discussi fino al 1955, quando ognuno di loro lasciò il Laboratorio di Fisica Applicata della Johns Hopkins University. La maggioranza della comunità astronomica, tuttavia, non era ancora particolarmente interessata ai temi della cosmologia. La predizione di Alpher e Herman fu riscoperta da Yakov Zel'dovich all'inizio degli anni 1960, e indipendentemente predetta da Robert Dicke contemporaneamente. La prima pubblicazione della radiazione di fondo come un fenomeno rilevabile apparve in un breve elaborato degli astrofisici sovietici A. G. Doroshkevich e Igor Novikov, nella primavera del 1964.[39] Nel 1964, David Todd Wilkinson e Peter Roll, colleghi di Robert Dicke all'Università di Princeton, iniziarono la costruzione di un radiometro Dicke per misurare la radiazione cosmica di fondo.[40] Nel 1965, Arno Penzias e Robert Woodrow Wilson ai Bell Laboratories nelle vicinanze di Holmdel Township, New Jersey, costruirono un radiometro Dicke che intendevano utilizzare per la radioastronomia e gli esperimenti di comunicazione via satellite. Tale strumento soffriva di un eccesso di temperatura dell'antenna di 3,5 K che non riuscivano a spiegare. Dopo aver ricevuto una telefonata proveniente da Crawford Hill, Dicke disse una frase che divenne famosa: "Boys, we've been scooped" (che in italiano suonerebbe più o meno come "Ragazzi, ci hanno rubato lo scoop!").[1][41][42] Una riunione tra i gruppi di Princeton e Crawford Hill stabilì che la temperatura di disturbo dell'antenna era effettivamente dovuta dalla radiazione cosmica di fondo. Penzias e Wilson ricevettero il Premio Nobel per la fisica nel 1978 per tale scoperta.[43]
L'interpretazione della radiazione cosmica di fondo fu oggetto di controversia negli anni 1960 con alcuni sostenitori della teoria dello stato stazionario, i quali sostenevano che la radiazione di fondo è il risultato della luce stellare riflessa dalle galassie lontane.[44] Utilizzando questo modello, e sulla base dello studio delle caratteristiche delle linee di assorbimento negli spettri delle stelle, l'astronomo Andrew McKellar ha scritto nel 1941: "Si può calcolare che la temperatura rotazionale dello spazio interstellare è di 2 K".[21][45] Secondo un'altra possibile interpretazione, utilizzando l'equazione del trasporto radiativo in coordinate polari si può dimostrare che la radiazione cosmica di fondo non è di origine extragalattica ma è di origine locale.[46][47] Tuttavia, durante gli anni 1970 venne stabilito che la radiazione cosmica di fondo è un residuo del Big Bang. Questo perché nuove misurazioni in una gamma di frequenze dello spettro hanno mostrato che era uno spettro di corpo nero termico, un risultato che il modello dello stato stazionario non riusciva a riprodurre.[48]

L'antenna con la quale Penzias e Wilson scoprirono la radiazione cosmica di fondo a Holmdel, nel New Jersey.
Harrison, Peebles, Yu e Zel'dovich si resero conto che l'universo primordiale avrebbe dovuto avere qualche disomogeneità a livello di 10−4 o 10−5.[49][50][51]Rashid Sunyaev poi calcolò l'impronta osservabile che tali disomogeneità avrebbero sulla radiazione cosmica di fondo.[52] Limiti sempre più stretti sull'anisotropia della radiazione cosmica di fondo sono stati stabiliti da esperimenti da terra, anche se l'anisotropia è stata innanzitutto rilevata attraverso l'analisi dei dati del RELIKT-1[29][53], come è stato riportato nel gennaio del 1992. A causa del ritardo plurimensile nella pubblicazione formale da parte delle riviste specializzate, il premio Nobel per la fisica per il 2006 venne assegnato al team del COBE, che rilevò le anisotropie tramite un radiometro differenziale a microonde pochi mesi dopo.[54][55]
Ispirato dai risultati di RELIKT-1 e COBE, nel decennio successivo una serie di esperimenti da terra e da pallone aerostatico misureranno la radiazione di fondo su scale angolari più piccole. L'obiettivo primario di questi esperimenti è stato quello di misurare l'entità del primo picco acustico, dato che il COBE non aveva una risoluzione sufficiente per studiarlo a fondo. Questo picco corrisponde a variazioni di densità su grande scala nell'universo primordiale, che vengono creati da instabilità gravitazionale, con conseguenti oscillazioni acustiche nel plasma.[56] Il primo picco nell'anisotropia è stata provvisoriamente individuata dal QMAP e il risultato è stato confermato dal BOOMERanG e dal MAXIMA.[57][58][59] Queste misurazioni hanno dimostrato che la forma dell'universo è approssimativamente piatta, piuttosto che curva.[60] Esse escludono le stringhe cosmiche come componente principale della formazione delle strutture cosmiche, e suggeriscono che l'inflazione cosmologica è la teoria giusta per spiegare la formazione delle strutture.[61]
Il secondo picco è stato provvisoriamente rilevato da diversi esperimenti, prima di essere definitivamente rilevato dal WMAP, che ha anche rilevato il terzo picco.[62] Al 2010, alcuni esperimenti per migliorare la misurazione della polarizzazione e la radiazione di fondo su piccole scale angolari sono ancora in corso. Questi includono DASI, WMAP, BOOMERanG, Planck Surveyor, Atacama Cosmology Telescope, South Pole Telescope e il telescopio QUIET.
Relazioni con il Big Bang |

Immagine delle anisotropie della radiazione di fondo dal WMAP.
Le misurazioni della radiazione cosmica di fondo hanno fatto della teoria inflazionistica del Big Bang il modello standard delle origini dell'universo.[63] Questa teoria prevede che le condizioni iniziali per l'universo siano di natura casuale (vale a dire che non si è in grado di risalire agli istanti precedenti ad esse), e seguano una distribuzione di probabilità approssimativamente gaussiana, rappresentata graficamente, a sezioni trasversali, da curve a forma di campana.
Analizzando questa distribuzione a diverse frequenze, viene generata una densità spettrale, o spettro di potenza. Lo spettro di potenza di queste fluttuazioni è stato calcolato e concorda con le osservazioni, anche se alcuni parametri, come ad esempio l'ampiezza complessiva delle fluttuazioni, sono parametri più o meno liberi del modello dell'inflazione cosmica.[64] Pertanto, le componenti più significative delle disomogeneità nell'universo devono essere di natura statistica.
Questo porta a una varianza cosmica, in cui le incertezze nella varianza delle fluttuazioni osservate su grande scala nell'universo sono difficili da comparare con precisione alla teoria. Il modello utilizza un campo gaussiano casuale con uno spettro di Harrison-Zel'dovich, o a invarianza di scala, per rappresentare le disomogeneità primordiali.[65]
Temperatura |
La radiazione cosmica di fondo e lo spostamento verso il rosso cosmologico sono considerati le migliori prove disponibili per la teoria del Big Bang. La scoperta della CMB nella metà degli anni 1960 fece scemare l'interesse verso soluzioni alternative come la teoria dello stato stazionario.[66]
La radiazione di fondo offre un'istantanea dell'universo, quando, secondo la cosmologia standard, la temperatura era scesa abbastanza da permettere la formazione di atomi di idrogeno da parte di elettroni e protoni, rendendo così l'universo trasparente alle radiazioni. Quando questo avvenne, circa 380.000 anni dopo il Big Bang (periodo conosciuto come periodo di ultimo scattering, successivo al periodo di ricombinazione nel quale si formarono i primi atomi stabili di idrogeno ed elio, e al periodo di disaccoppiamento nel quale la radiazione presente nell'universo cessò di interagire con la materia), la temperatura dell'Universo era di circa 3.000 K. Ciò corrisponde ad una energia di circa 0,25 eV, che è molto inferiore ai 13,6 eV, ovvero l'energia di ionizzazione dell'idrogeno.[67]
Dal momento del disaccoppiamento, la temperatura della radiazione di fondo è scesa di circa 1.100 volte[68] a causa dell'espansione dell'universo. Come conseguenza dell'espansione, i fotoni della CMB si spostano verso il rosso, rendendo la temperatura della radiazione inversamente proporzionale ad un parametro chiamato fattore di scala dell'universo. Si può dimostrare che l'andamento della temperatura Tr della CMB in funzione dello spostamento verso il rosso, z, è proporzionale alla temperatura della CMB attuale (2,728 K o 0,235 meV) secondo la seguente relazione:
- Tr=2,728(1+z){displaystyle {mathit {T}}_{r}=2{,}728(1+{mathit {z}})}
Spettro di potenza |
Lo strumento matematico che consente di studiare le anisotropie di temperatura è lo sviluppo in armoniche sferiche Ylm(θ,ϕ){displaystyle Y_{lm}(theta ,phi )}

- ΔT(θ,ϕ)=∑lmalmYlm(θ,ϕ)l=1…+∞;−l≤m≤l;{displaystyle Delta T(theta ,phi )=sum _{lm}a_{lm}Y_{lm}(theta ,phi )qquad l=1ldots +infty ;qquad -lleq mleq l;}
dove θ{displaystyle theta }











Anisotropie della CMB |
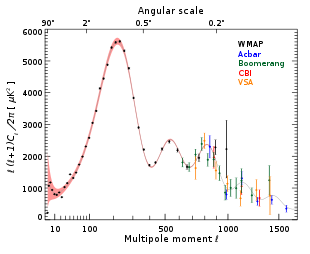
Spettro di potenza delle anisotropie di temperatura della CMB in termini di scala angolare (o momenti di multipolo). La linea continua mostra l'andamento teorico mentre i punti rappresentano i dati sperimentali. I dati provengono dalle sonde WMAP (2006), Acbar (2004) Boomerang (2005), CBI (2004), e VSA (2004).
La radiazione cosmica di fondo presenta un'alta isotropia, indice di una notevole omogeneità del plasma primordiale. Tale omogeneità però non avrebbe portato alla creazione di strutture come galassie e ammassi. La presenza di questi oggetti implica delle anisotropie del plasma.
La CMB presenta due tipologie di anisotropie, chiamate primarie e secondarie.
Anisotropie primarie |
L'anisotropia della radiazione cosmica di fondo è divisa in due tipi: anisotropia primaria, derivante dagli effetti che si verificano sulla superficie di ultimo scattering e prima, e anisotropia secondaria, legata ad effetti quali le interazioni con il gas caldo o il potenziale gravitazionale, tra la superficie di ultimo scattering e l'osservatore.
La struttura delle anisotropie è determinata principalmente da due effetti: oscillazioni acustiche e smorzamento della diffusione (noto anche come smorzamento senza collisione). Le oscillazioni acustiche sorgono a causa della competizione tra fotoni e barioni nel plasma dell'universo primordiale. La pressione dei fotoni tende a cancellare le anisotropie, mentre l'attrazione gravitazionale dei barioni, in movimento a velocità molto più basse della luce, li porta a collassare formando così densi aloni. Questi due effetti sono in competizione tra loro, creando le oscillazioni acustiche che danno al fondo a microonde la sua caratteristica struttura a picchi. I picchi corrispondono, grosso modo, alle risonanze alle quali i fotoni si dissociano quando un particolare modo di oscillazione è al suo picco di ampiezza.
I picchi contengono interessanti impronte fisiche. La scala angolare del primo picco determina la curvatura dell'universo (ma non la sua topologia). Il picco successivo (che è il rapporto tra i picchi pari e i picchi dispari) determina la ridotta densità barionica. Il terzo picco può essere utilizzato per estrarre informazioni sulla densità di materia oscura.
Le posizioni dei picchi danno anche importanti informazioni sulla natura delle perturbazioni primordiali della densità. Ci sono due tipologie fondamentali di perturbazioni della densità, le adiabatiche e quelle a isocurvatura. Una generica perturbazione di densità è un misto di entrambe, e le differenti teorie che pretendono di spiegare lo spettro della perturbazione primordiale della densità prevedono miscele differenti.
- Perturbazioni adiabatiche della densità
- la superdensità frazionale in ogni componente della materia (barioni, fotoni ...) è la stessa. Ovvero, se c'è l'1% in più di energia nei barioni rispetto alla media in un dato posto, allora per una perturbazione di densità adiabatica pura c'è anche l'1% in più di energia nei fotoni, e l'1% di energia in più nei neutrini, rispetto alla media. L'inflazione cosmologica prevede che le perturbazioni primordiali siano adiabatiche.
- Perturbazioni di isocurvatura nella densità
- la somma delle superdensità frazionali è pari a zero. Ovvero, una perturbazione in cui in un certo punto vi è l'1% in più di energia nei barioni rispetto alla media, l'1% in più di energia in fotoni rispetto alla media, e il 2% di energia in meno nei neutrini rispetto alla media, sarebbe una perturbazione di isocurvatura pura. Le stringhe cosmiche dovrebbero produrre per lo più perturbazioni primordiali a isocurvatura.
Lo spettro della CMB è in grado di distinguerle, perché queste due diverse tipologie di perturbazioni danno luogo a differenti localizzazioni dei picchi. Le perturbazioni di isocurvatura della densità producono una serie di picchi la cui scala angolare (il valore l dei picchi) è all'incirca in rapporti 1:3:5:... mentre le perturbazioni adiabatiche producono picchi le cui localizzazioni sono in rapporti 1:2:3:...[69] Le osservazioni corrispondono a quanto ci si può attendere da perturbazioni di densità primordiale completamente adiabatiche, fornendo un supporto chiave per la teoria inflazionistica, ed escludendo molti modelli di contemplano la formazione di strutture, come ad esempio le stringhe cosmiche.
Lo smorzamento senza collisioni è causato da due effetti, che sorgono quando il trattamento del plasma primordiale come fluido comincia a non essere più valido:
- L'aumento del cammino libero medio dei fotoni mentre il plasma primordiale diventa sempre più rarefatto nell'universo in espansione;
- La profondità finita della superficie di ultimo scattering, che fa sì che il cammino libero medio cresca rapidamente durante il disaccoppiamento, anche se qualche scattering Compton è ancora in corso.
Questi effetti contribuiscono quasi equamente alla soppressione delle anisotropie su scale piccole, e danno origine alla caratteristica coda di smorzamento esponenziale visibile nelle anisotropie su scala angolare piccolissima.
La profondità della superficie di ultimo scattering si riferisce al fatto che il disaccoppiamento dei fotoni e barioni non avviene istantaneamente, ma richiede invece una frazione apprezzabile di età dell'Universo fino a tale epoca. Un metodo per quantificare esattamente quanto lungo sia questo processo è la funzione di visibilità del fotone (photon visibility function, PVF). Questa funzione è definita in modo che, denotando la PVF con P(t), la probabilità che un fotone della CMB abbia avuto l'ultimo scattering tra il tempo t e t+dt{displaystyle t+dt}

Il massimo della PVF (il momento più probabile in cui è avvenuto l'ultimo scattering di un dato fotone della CMB) è noto con una certa precisione. I risultati del primo anno di osservazioni del WMAP situano il momento in cui P(t) è al massimo a 372 ± 14 ka[70]. Questo è spesso considerato come il momento della nascita della radiazione di fondo. Tuttavia, per capire "quanto" tempo ci hanno messo fotoni e barioni a disaccoppiarsi, occorre avere anche una misura della larghezza della PVF. Il team del WMAP ritiene che la PVF sia maggiore della metà del suo valore massimo (la "piena larghezza a metà altezza", o FWHM[71][72]), in un intervallo di 115 ± 5 ka. In base a questa misura, il disaccoppiamento ha avuto luogo in circa 115 000 anni, e quando fu terminato, l'universo aveva circa 487 000 anni di età.
Anisotropie secondarie |
Da quanto si può osservare la radiazione di fondo, a partire dal momento della sua formazione, è stata modificata da diversi processi fisici successivi, che sono indicati collettivamente con il nome di anisotropie successive o anisotropie secondarie.
Quando i fotoni della CMB sono stati liberi di viaggiare senza ostacoli, la materia ordinaria dell'universo consisteva per lo più di atomi di idrogeno e di elio neutri. Tuttavia, le osservazioni odierne delle galassie sembrano indicare che la maggior parte del volume dello spazio intergalattico è costituito da materiale ionizzato (in quanto ci sono poche linee di assorbimento derivanti da atomi di idrogeno). Questo implica un periodo di reionizzazione durante il quale una parte del materiale dell'universo venne frammentata in ioni di idrogeno.

E polarization measurements as of March 2008 in terms of angular scale (or multipole moment). The polarization is much more poorly measured than the temperature anisotropy.
I fotoni della CMB dispersero le cariche libere, come gli elettroni non legati ad atomi. In un universo ionizzato, queste particelle cariche sono state liberate dagli atomi neutri dalle radiazioni ionizzanti come i raggi ultravioletti. Oggi queste cariche libere hanno una densità sufficientemente bassa nella maggior parte del volume dell'Universo, da non incidere apprezzabilmente sulla CMB. Tuttavia, se il mezzo interstellare è stato ionizzato in un'era sufficientemente primordiale, quando l'universo era ancora molto più denso, ci sono due effetti principali sulla radiazione di fondo:
- Le anisotropie su piccola scala vengono cancellate (come quando guardando un oggetto attraverso la nebbia, i dettagli degli oggetti appaiono sfocati.)
- La fisica di come i fotoni vengono diffusi dagli elettroni liberi (scattering Thomson) induce un'anisotropia di polarizzazione su grandi scale angolari. Questa polarizzazione su ampio angolo è correlata con la perturbazione della temperatura di ampio angolo.
Entrambi gli effetti sono stati osservati dal WMAP, fornendo la prova che l'universo è stato ionizzato molto presto, ad un redshift superiore a 17. La provenienza dettagliata di queste radiazioni ionizzanti è ancora oggetto di dibattito scientifico. Potrebbero includere luce stellare dalle primissime stelle (stelle di popolazione III), supernovae, quando queste stelle raggiunsero la fine della loro vita, o le radiazioni ionizzanti prodotte dai dischi di accrescimento di buchi neri massicci.
Il momento successivo all'emissione della radiazione cosmica di fondo, e prima dell'osservazione delle prime stelle, viene chiamato umoristicamente dagli astronomi era oscura (dark age)[73], ed è un periodo che è in fase di intenso studio da parte degli astronomi (riga a 21 cm dell'idrogeno neutro).
Altri due effetti che si verificarono tra la reionizzazione e le attuali osservazioni della radiazione cosmica di fondo, e che sembrano provocare anisotropie, includono l'effetto Sunyaev-Zel'dovich, dove una nube di elettroni ad alta energia diffonde la radiazione trasferendo parte della sua energia ai fotoni della CMB, e l'effetto Sachs-Wolfe, che provoca ai fotoni della radiazione cosmica di fondo uno spostamento gravitazionale verso il rosso o verso il blu, a causa del cambiamento del campo gravitazionale.
Anisotropia di dipolo |

Mappe della CMB registrate dal satellite COBE. La prima in alto mostra l'anisotropia di dipolo, quella centrale l'emissione galattica mentre l'ultima mostra esclusivamente il segnale di CMB.
Questa anisotropia non è di natura intrinseca ma è dovuta al moto del nostro sistema di riferimento (il sistema solare) rispetto al sistema di riferimento della radiazione di fondo che può essere considerato come un sistema in quiete.
Questa anisotropia è di ampiezza maggiore rispetto alle altre ed è ad una temperatura di 3,353±0,024 mK.
Polarizzazione |
La radiazione cosmica di fondo è polarizzata a livello di qualche microkelvin. Esistono due tipi di polarizzazione, chiamati E-mode e B-mode. Questo un'analogia con l'elettrostatica, in cui il campo elettrico (campo E) ha un rotore nullo, e il campo magnetico (campo B) ha una divergenza nulla. Gli E-mode sorgono naturalmente dallo scattering Thomson in un plasma eterogeneo. I B-mode, che non sono stati misurati e si pensa abbiano un'ampiezza massima di 0,1 µK, non sono prodotti solo dalla fisica del plasma. Si tratta di un segnale proveniente dall'inflazione cosmica e sono determinati dalla densità delle onde gravitazionali primordiali. Il rilevamento del segnale B-mode sarà estremamente difficile, tanto più che il grado di contaminazione di primo piano è sconosciuto, e il segnale di lente gravitazionale debole mescola il segnale relativamente forte E-mode con il segnale B-mode[74].
Le anisotropie di quadrupolo hanno ordine di multipolo l=2{displaystyle l=2}

Perturbazioni scalari (m=0) {displaystyle (m=0) }: le fluttuazioni di densità di energia nel plasma causano un gradiente nella distribuzione della velocità.
Perturbazioni vettoriali (m=±1){displaystyle (m=pm 1)}: la vorticosità del plasma crea un differente tipo di quadrupolo dovuto allo spostamento Doppler con la velocità. Tale vorticosità sarebbe però stata smorzata durante l'inflazione e ci si aspetta sia trascurabile.
Perturbazioni tensoriali (m=±2){displaystyle (m=pm 2)}: le onde gravitazionali modificano lo spazio che contiene i fotoni nelle direzioni ortogonali attraversando il plasma. Inoltre modificano la lunghezza d'onda della radiazione creando anche anisotropie quadrupolari di temperatura.

Polarizzazione E-mode in termini di scala angolare. La polarizzazione viene misurata meno precisamente rispetto alle anisotropie della temperatura. (Marzo 2008)
Osservazioni della radiazione di fondo |
.mw-parser-output .vedi-anche{border:1px solid #CCC;font-size:95%;margin-bottom:.5em}.mw-parser-output .vedi-anche td:first-child{padding:0 .5em}.mw-parser-output .vedi-anche td:last-child{width:100%}
Dopo la scoperta della radiazione di fondo, sono stati condotti centinaia di esperimenti per misurare e caratterizzare i segnali caratteristici della radiazione. L'esperimento più famoso è probabilmente il COBE della NASA, satellite che orbitò dal 1989 al 1996, il quale individuò e quantificò le anisotropie su larga scala al limite delle sue capacità di rilevazione. Ispirata dai risultati del COBE che mostravano una CMB estremamente isotropa e omogenea, nel corso di un decennio una serie di esperimenti a terra e su pallone ha permesso di quantificare le anisotropie con ulteriori misure su scala angolare più piccola.
L'obiettivo primario di questi esperimenti era di misurare l'entità angolare del primo picco acustico, per la quale il COBE non aveva una risoluzione sufficiente. Queste misurazioni sono state in grado di escludere le stringhe cosmiche come la teoria principale di formazione delle strutture cosmiche, e hanno suggerito che l'inflazione cosmica era la teoria giusta. Negli anni 1990, il primo picco è stato misurato con una sensibilità crescente e verso il 2000 l'esperimento BOOMERanG ha rilevato che le fluttuazioni di potenza massima si verificano su scale di circa un grado. Insieme ad altri dati cosmologici, questi risultati implicano che la geometria dell'universo è piatta. Nei tre anni successivi un certo numero di interferometri terrestri, tra cui il telescopio VSA, il DASI e il CBI, hanno fornito misurazioni delle oscillazioni con una maggiore precisione. Il DASI ha effettuato la prima rilevazione della polarizzazione della CMB e il CBI ha fornito il primo spettro di polarizzazione E-mode con una prova convincente che è fuori fase rispetto allo spettro T-mode.
Nel giugno del 2001, la NASA ha lanciato una seconda missione spaziale per la CMB, la Wilkinson microwave anisotropy probe (WMAP), per effettuare misurazioni molto più precise delle anisotropie su grande scala con una mappatura completa del cielo. I primi dati diffusi dalla missione nel 2003, erano misure dettagliate dello spettro di potenza su scale inferiori a un grado. I risultati sono sostanzialmente coerenti con quelli previsti dall'inflazione cosmica e da altre diverse teorie, e sono disponibili in dettaglio nella banca dati della NASA per la radiazione cosmica di fondo (CMB). Anche se il WMAP ha fornito misurazioni molto accurate della fluttuazione su grande scala angolare della CMB, non ha avuto una risoluzione angolare sufficiente per misurare le fluttuazioni su scala minore osservate da terra da altri esperimenti.
Una terza missione spaziale, il Planck Surveyor, è stato lanciato nel maggio del 2009. Planck si avvale sia di radiometri HEMT sia di bolometri, ed è in grado di misurare la CMB su scale più piccole del WMAP. A differenza delle due precedenti missioni spaziali, Planck è gestito dall'ESA, l'Agenzia spaziale europea. I suoi rilevatori hanno effettuato un test di prova sul telescopio antartico Viper con l'esperimento ACBAR, che ha prodotto le misurazioni più precise alle piccole scale angolari fino ad oggi, e sul telescopio Archeops, montato su un pallone. La missione si è conclusa nel 2013. Le immagini della radiazione cosmica di fondo prodotte dal satellite Planck[75] sono in accordo con quelle ottenute dal satellite WMAP e confermano i dati precedenti, ma con una precisione maggiore (5 milioni di pixel di risoluzione contro i 3 milioni di WMAP)[76].
Altri strumenti basati a terra, come il South Pole Telescope in Antartide, il telescopio Clover, l'Atacama Cosmology Telescope e il telescopio QUIET in Cile dovrebbero fornire i dati non ottennibili da osservazioni satellitari, e forse anche la polarizzazione B-mode.
Riduzione e analisi dei dati |
I dati grezzi provenienti dalle sonde spaziali (come il WMAP) contengono effetti di primo piano che oscurano completamente la struttura a scala fine della radiazione di fondo a microonde. La struttura fine è sovrapposta ai dati grezzi della CMB, ma è troppo piccola per essere rilevata alla scala dei dati grezzi. Il più importante degli effetti di primo piano è l'anisotropia di dipolo causata dal moto del Sole rispetto alla CMB. Le anisotropie di dipolo e di altro tipo, causate dal moto annuale della Terra rispetto al Sole, insieme a numerose altre fonti di radiazioni a microonde provenienti dal piano galattico ed extragalattico, devono essere sottratte per rendere evidenti le variazioni molto piccole che caratterizzano la struttura a scala fine della CMB.
L'analisi in dettaglio dei dati CMB per produrre mappe, uno spettro di potenza angolare e, infine, i parametri cosmologici è un problema computazionalmente difficile. Sebbene la computazione di uno spettro di potenza da una mappa è in linea di principio una semplice trasformata di Fourier, scomponendo la mappa del cielo in armoniche sferiche, in pratica però è difficile tener conto degli effetti del rumore e delle fonti di primo piano. In particolare, il primo piano è dominato da emissioni galattiche come le Bremsstrahlung, le radiazioni di sincrotrone, e le polveri che emettono segnali nella banda delle microonde. In pratica, le radiazioni provenienti dalla nostra Galassia devono essere eliminate, dando luogo a una mappatura che non contempla più l'intero cielo. Inoltre, sorgenti puntiformi come galassie e ammassi rappresentano altre fonti di primo piano che devono essere rimosse affinché non distorcano la struttura su scala piccola dello spettro di potenza della CMB.
Le restrizioni che gravano su molti parametri cosmologici possono essere ricavate dai loro effetti sullo spettro di potenza, ed i risultati sono spesso calcolati utilizzando le tecniche di campionamento Markov Chain Monte Carlo.
Sulla base di alcune anomalie osservate da Planck Surveyor (come una differenza significativa nel segnale osservato nei due emisferi opposti del cielo, e una regione fredda eccessivamente grande, tale da dover accettare l'esistenza di un enorme supervuoto), taluni hanno ipotizzato che la radiazione potesse essere un fenomeno più locale e quindi non un residuo del Big Bang[77]; in passato era stato obiettato che la sua origine fosse nell'estinzione interstellare con presenza di particelle di ferro sullo sfondo[78] (Hoyle, Narlikar, Arp) o una radiazione polarizzata di sincrotrone proveniente da radiogalassie e radiosorgenti lontane e annichilazioni materia-antimateria (Cosmologia del plasma).
Anisotropie di dipolo |
Dai dati dalla radiazione di fondo si vede che il nostro gruppo locale di galassie (l'ammasso galattico che include la Via Lattea), sembra muoversi a 627 ± 22 km/s rispetto al sistema di riferimento della CMB in direzione della longitudine galattica l = 276±3°, b = 30±3º.[79] Questo movimento provoca un'anisotropia dei dati in quanto la CMB appare leggermente più calda nella direzione del movimento che nella direzione opposta.[80] L'interpretazione standard di queste variazioni di temperatura è un semplice spostamento verso il rosso e verso il blu dovuto al moto relativo rispetto alla CMB, ma modelli cosmologici alternativi sono in grado di spiegare alcune frazioni della distribuzione della temperatura di dipolo osservate nella CMB.[81]
Multipoli a basso valore di «l» ed altre anomalie |
Con i dati sempre più precisi forniti dal WMAP, ci sono state una serie di segnalazioni secondo cui la CMB soffre di anomalie, come anisotropie su grandissima scala, allineamenti anomali, e distribuzioni non-gaussiane.[82][83][84][85]
La più duratura di queste è la polemica sui multipoli a bassi valori di l. Anche nella mappa del COBE si è osservato che il quadrupolo (l = 2, armoniche sferiche) ha un'ampiezza bassa rispetto alle previsioni del Big Bang. Alcuni osservatori hanno fatto notare che le anisotropie nei dati del WMAP non sembrano essere coerenti con il quadro del big bang. In particolare, il quadrupolo e l'octupolo (l = 3) sembrano avere un allineamento inspiegabile tra di loro e con il piano dell'eclittica,[86][87][88] un allineamento a volte indicato come l'asse del male[83][89].
Alcuni gruppi hanno suggerito che questo potrebbe rappresentare l'indicazione di una nuova fisica alle scale più grandi osservabili.
In ultima analisi, a causa degli effetto di primo piano e del problema della varianza cosmica, le modalità più grandi non saranno mai misurabili così precisamente come le modalità a piccola scala angolare. Le analisi sono state effettuate su due mappe dalle quali i primi piani sono stati rimossi nel miglior modo possibile: la mappa della «combinazione lineare interna» del WMAP e una mappa simile preparata da Max Tegmark e altri.[62][68][90] Analisi successive hanno evidenziato che queste sono le modalità più sensibili alla contaminazione di primo piano delle radiazioni da sincrotrone, polveri, bremsstrahlung, e da incertezze sperimentali nel monopolo e nel dipolo. Un'analisi bayesiana dello spettro di potenza del WMAP dimostra che la previsione del quadrupolo del modello cosmologico Lambda-CDM è coerente con i dati al livello del 10% e che l'octupolo osservato non è notevole[91]. Conti più attenti sulla procedura utilizzata per rimuovere il primo piano dalla mappatura completa del cielo, riducono ulteriormente l'importanza dell'allineamento del 5% circa.[92][93][94][95]
Note |
^ ab (EN) A.A. Penzias, R.W. Wilson, A Measurement of Excess Antenna Temperature at 4080 Mc/s, in Astrophysical Journal, vol. 142, 1965, pp. 419–421, DOI:10.1086/148307.
^ (EN) Smoot Group, The Cosmic Microwave Background Radiation, aether.lbl.gov, 28 marzo 1996. URL consultato l'11 dicembre 2008.
^ Questo vale se si misura l'intensità per unità di frequenza, secondo la legge di Planck. Se invece la si misura per unità di lunghezza d'onda, utilizzando la legge di Wien, il picco sarà a 1,06 millimetri corrispondenti ad una frequenza di 283 gigahertz.
^ ab (EN)
M. White, Anisotropies in the CMB, 1999 Meeting of the Division of Particles and Fields of the American Physical Society, Los Angeles, University of California, 1999, arΧiv:astro-ph/9903232. URL consultato il 15 luglio 2010.
^
(EN) E.L. Wright, Theoretical Overview of Cosmic Microwave Background Anisotropy, in Measuring and Modeling the Universe, Cambridge University Press, 2004, p. 291, ISBN 0-521-75576-X, arΧiv:astro-ph/0305591.accessorichiedeurl(aiuto)
^ Dopo che è stata sottratta l'anisotropia di dipolo dovuta all'effetto Doppler della radiazione di fondo, causata dalla nostra velocità peculiare rispetto alla struttura dell'universo in coordinate comoventi. Questa correzione è coerente con il fatto che la Terra si muove a circa 627 km/s verso la costellazione della Vergine.
^ (EN) D. J. Fixsen et al., The Cosmic Microwave Background Spectrum from the full COBE FIRAS data set, in Astrophysical Journal, vol. 473, 1996, pp. 576–587, DOI:10.1086/178173.accessorichiedeurl(aiuto)
^
A. H. Guth, The Inflationary Universe: The Quest for a New Theory of Cosmic Origins, Basic Books, 1998, ISBN 0-201-32840-2.
^ Le poche eccezioni sono le disomogeneità derivanti dalle fluttuazioni quantistiche nel campo inflazionario.
^
(EN) D. Cirigliano, de Vega, H.J.; Sanchez, N.G., Clarifying inflation models: The precise inflationary potential from effective field theory and the WMAP data, in Physical Review D, vol. 71, nº 10, 2005, pp. 77–115, DOI:10.1103/PhysRevD.71.103518, arΧiv:astro-ph/0412634.
^
(EN) B. Abbott, Microwave (WMAP) All-Sky Survey, Hayden Planetarium, 2007. URL consultato il 16 luglio 2010.
^ Equivale ad un redshift di z = 1,088.
^
(EN) E. Gawiser, Silk, J., The cosmic microwave background radiation, in Physics Reports, 333–334, 2000, p. 245, DOI:10.1016/S0370-1573(00)00025-9, arΧiv:astro-ph/0002044.
^ (EN) G. F. Smoot, Cosmic Microwave Background Radiation Anisotropies: Their Discovery and Utilization, su Nobel Lecture, Nobel Foundation, 2006. URL consultato il 1º agosto 2010.
^ (EN) E. Komatsu, Scientists say universe is 20M years older, http://www.itwire.com/, 2010. URL consultato il 1º agosto 2010.
^ (EN) Charles H. Lineweaver, Tamara M. Davis, Misconceptions about the Big Bang, in Scientific American, marzo 2005. URL consultato il 1º agosto 2010.
^ (EN) E.R. Harrison, Cosmology, Cambridge, Cambridge University Press, 2000, pp. 446–448, ISBN 0-521-66148-X.
^ (EN) M.P. Hobson, Efstathiou, G., Lasenby, A.N., General Relativity: An Introduction for Physicists, Cambridge, Cambridge University Press, 2006, p. 338, ISBN 0-521-82951-8.
^ La densità dei fotoni è di 4,7×10−31 kg/m³, mentre la densità critica è di 7,9×10−27 kg/m³. Il rapporto tra i due è di 5,9×10−5. Si veda A. Unsöld e B. Bodo, The New Cosmos, An Introduction to Astronomy and Astrophysics, 5th, Springer Verlag, 2002, p. 485, ISBN 3-540-67877-8.
^ ab
D.N. Spergel et al., First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters, in Astrophysical Journal (Supplement Series), vol. 148, nº 1, 2003, pp. 175–194, DOI:10.1086/377226, arΧiv:astro-ph/0302209.
^ ab
A. McKellar, Molecular Lines from the Lowest States of Diatomic Molecules Composed of Atoms Probably Present in Interstellar Space, in Publications of the Dominion Astrophysical Observatory (Victoria, BC), vol. 7, 1941, pp. 251–272.
^
S. Weinberg, Oxford Astronomy Encyclopedia, John Wiley & Sons, 1972, p. 514, ISBN 0-471-92567-5.
^ abcde H. Kragh, Cosmology and Controversy: The Historical Development of Two Theories of the Universe, Princeton University Press, 1999, p. 135, ISBN 0-691-00546-X. "In 1946, Robert Dicke and coworkers at MIT tested equipment that could test a cosmic microwave background of intensity corresponding to about 20K in the microwave region. However, they did not refer to such a background, but only to 'radiation from cosmic matter'. Also, this work was unrelated to cosmology and is only mentioned because it suggests that by 1950, detection of the background radiation might have been technically possible, and also because of Dicke's later role in the discovery". Vedi anche R. H. Dicke et al., Atmospheric Absorption Measurements with a Microwave Radiometer, in Physical Review, vol. 70, 5–6, 1946, pp. 340–348, DOI:10.1103/PhysRev.70.340.
^
G. Gamow, Cosmology and Controversy: The Historical Development of Two Theories of the Universe, Courier Dover Publications, 2004 [1961], p. 40, ISBN 0-486-43868-6.
^ Kragh, H. (1999:132). "Alpher and Herman first calculated the present temperature of the decoupled primordial radiation in 1948, when they reported a value of 5 K. Although it was not mentioned either then or in later publications that the radiation is in the microwave region, this follows immediately from the temperature... Alpher and Herman made it clear that what they had called "the temperature in the universe" the previous year referred to a blackbody distributed background radiation quite different from sunlight".
^ (RU) T. A. Shmaonov, Commentary, in Pribory i Tekhnika Experimenta, vol. 1, 1957, p. 83, DOI:10.1016/S0890-5096(06)60772-3.
^ P. D. Naselsky, D.I. Novikov e I. D. Novikov, The Physics of the Cosmic Microwave Background, Cambridge University Press, 2006, p. 5, ISBN 0-521-85550-0.
^ A. G. Doroshkevich e I.D. Novikov, Mean Density of Radiation in the Metagalaxy and Certain Problems in Relativistic Cosmology, in Soviet Physics Doklady, vol. 9, 1964, Bibcode:1964SPhD....9..111D.
^ ab Y. Zaitsev, Nobel Prize In Physics: Russia's Missed Opportunities, RIA Novosti, 21 novembre 2006. URL consultato l'11 dicembre 2008.
^ R. Sanders, Kahn, J., UC Berkeley, LBNL cosmologist George F. Smoot awarded 2006 Nobel Prize in Physics, UC Berkeley News, 13 ottobre 2006. URL consultato l'11 dicembre 2008.
^
J.M. Kovac et al., Detection of polarization in the cosmic microwave background using DASI, in Nature, vol. 420, nº 6917, 2002, pp. 772–787, DOI:10.1038/nature01269, PMID 12490941.
^
A. C. S. Readhead et al., Polarization Observations with the Cosmic Background Imager, in Science, vol. 306, nº 5697, 2004, pp. 836–844, DOI:10.1126/science.1105598, PMID 15472038.
^
G. Gamow, The Origin of Elements and the Separation of Galaxies, in Physical Review, vol. 74, nº 4, 1948, pp. 505–506, DOI:10.1103/PhysRev.74.505.2.
^
G. Gamow, The evolution of the universe, in Nature, vol. 162, 1948, pp. 680–682, DOI:10.1038/162680a0.
^
R. A. Alpher e R. C. Herman, On the Relative Abundance of the Elements, in Physical Review, vol. 74, nº 12, 1948, pp. 1737–1742, DOI:10.1103/PhysRev.74.1737.
^ Questa stima è così elevata a causa di una sottostima della costante di Hubble da parte di Alfred Behr, che non poteva essere replicata, e fu in seguito abbandonata per la stima precedente.
^ Si veda la tabella della timeline.
^
A. K. T. Assis e M. C. D. Neves, History of the 2.7 K Temperature Prior to Penzias and Wilson (PDF), in Apeiron, vol. 2, nº 3, 1995, pp. 79–87. e si veda anche E. L. Wright, Eddington's Temperature of Space, UCLA, 2006. URL consultato l'11 dicembre 2008.
^ A. A. Penzias, The origin of elements (PDF), su Nobel lecture, Nobel Foundation, 2006. URL consultato il 4 ottobre 2006.
^
R. H. Dicke, The Measurement of Thermal Radiation at Microwave Frequencies, in Review of Scientific Instruments, vol. 17, 1946, pp. 268–275, DOI:10.1063/1.1770483. Questo schema di base per un radiometro è stato utilizzato nella maggior parte dei successivi esperimenti sulla radiazione cosmica di fondo.
^
R. H. Dicke et al., Cosmic Black-Body Radiation, in Astrophysical Journal, vol. 142, 1965, pp. 414–419, DOI:10.1086/148306.
^ Citato in P. J. E Peebles, Principles of Physical Cosmology, Princeton University Press, 1993, pp. 139–148, ISBN 0-691-01933-9.
^ The Nobel Prize in Physics 1978, Nobel Foundation, 1978. URL consultato l'8 gennaio 2009.
^
J. V. Narlikar e N. C. Wickramasinghe, Microwave Background in a Steady State Universe, in Nature, vol. 216, 1967, pp. 43–44, Bibcode:1967Natur.216...43N, DOI:10.1038/216043a0.
^ Nell'originale: It can be calculated that the rotational temperature of interstellar space is 2 K.
^ Perdita di energia della luce nello spazio interstellare e intergalattico
^ Solution of the transfer equation in a scattering atmosphere with spherical symmetry
^
P. J. E. Peebles et al., The case for the relativistic hot big bang cosmology, in Nature, vol. 352, 1991, pp. 769–776, Bibcode:1991Natur.352..769P, DOI:10.1038/352769a0.
^
E. R. Harrison, Fluctuations at the threshold of classical cosmology, in Physical Review D, vol. 1, 1970, pp. 2726–2730, DOI:10.1103/PhysRevD.1.2726.
^ P. J. E. Peebles e J. T. Yu, Primeval Adiabatic Perturbation in an Expanding Universe, in Astrophysical Journal, vol. 162, 1970, pp. 815–836, DOI:10.1086/150713.
^
Y. B. Zeldovich, A hypothesis, unifying the structure and the entropy of the Universe, in Monthly Notices of the Royal Astronomical Society, vol. 160, 1972, pp. 1P–4P, Bibcode:1972MNRAS.160P...1Z.
^
A.G. Doroshkevich, Y.B. Zel'Dovich, R.A. Syunyaev, The large scale structure of the universe; Proceedings of the Symposium, Fluctuations of the microwave background radiation in the adiabatic and entropic theories of galaxy formation, Tallinn, M. S. Longair e J. Einasto, 12-16 settembre 1977. Anche se questa è la prima pubblicazione a parlare delle disomogeneità della densità come anisotropie della radiazione cosmica di fondo, qualche premessa di base si può già trovare nel lavoro di Peebles e Yu già citato.
^ Dmitry Skulachev, History of relict radiation study: Soviet "RELIKT" and American "COBE", Izvestia Nauki (Science News). URL consultato il 28 maggio 2010 (archiviato dall'url originale il 27 giugno 2009).
^
G. F. Smooth et al., Structure in the COBE differential microwave radiometer first-year maps, in Astrophysical Journal Letters, vol. 396, nº 1, 1992, pp. L1–L5, DOI:10.1086/186504.
^
C.L. Bennett et al., Four-Year COBE DMR Cosmic Microwave Background Observations: Maps and Basic Results, in Astrophysical Journal Letters, vol. 464, 1996, pp. L1–L4, DOI:10.1086/310075.
^
C. Grupen et al., Astroparticle Physics, Springer, 2005, pp. 240–241, ISBN 3-540-25312-2.
^
A. D. Miller et al., A Measurement of the Angular Power Spectrum of the Microwave Background Made from the High Chilean Andes, in Astrophysical Journal, vol. 521, nº 2, 1999, pp. L79–L82, DOI:10.1086/312197.
^
A. Melchiorri et al., A Measurement of Ω from the North American Test Flight of Boomerang, in Astrophysical Journal, vol. 536, nº 2, 2000, pp. L63–L66, DOI:10.1086/312744.
^
S. Hanany et al., MAXIMA-1: A Measurement of the Cosmic Microwave Background Anisotropy on Angular Scales of 10'-5°, in Astrophysical Journal, vol. 545, nº 1, 2000, pp. L5–L9, DOI:10.1086/317322.
^
P. de Bernardis et al., A flat Universe from high-resolution maps of the cosmic microwave background radiation, in Nature, vol. 404, nº 6781, 2000, pp. 955–959, Bibcode:2000Natur.404..955D, DOI:10.1038/35010035, PMID 10801117.
^
L. Pogosian et al., Observational constraints on cosmic string production during brane inflation, in Physical Review D, vol. 68, nº 2, 2003, p. 023506, Bibcode:2003PhRvD..68b3506P, DOI:10.1103/PhysRevD.68.023506.
^ ab G. Hinshaw, et al. (WMAP collaboration), Three-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: temperature analysis, in Astrophysical Journal (Supplement Series), vol. 170, nº 2, 2007, pp. 288–334, DOI:10.1086/513698, arΧiv:astro-ph/0603451.
^ D. Scott, The Standard Cosmological Model, 2005, Bibcode:2005astro.ph.10731S, arΧiv:astro-ph/0510731.
^ M. S. Turner, The New Cosmology: Mid-term Report Card for Inflation, 2002, arΧiv:astro-ph/0212281
^ S. Torres, Topological Analysis of COBE-DMR CMB Maps, 1993, Imperial College Press, arΧiv:astro-ph/9311067, ISBN 1860945775
^ Durham, Frank; Purrington, Robert D., Frame of the universe: a history of physical cosmology, Columbia University Press, 1983, pp. 193–209, ISBN 0-231-05393-2.
^ Robert H. Brandenberger, Formation of Structure in the Universe, su adsabs.harvard.edu, 1995. URL consultato il 1º settembre 2009.
^ ab
C. L. Bennett, et al. (WMAP collaboration), First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: preliminary maps and basic results, in Astrophysical Journal (Supplement Series), vol. 148, 2003, p. 1, DOI:10.1086/377253, arΧiv:astro-ph/0302207. This paper warns, "the statistics of this internal linear combination map are complex and inappropriate for most CMB analyses."
^ W. Hu e M. White, Acoustic Signatures in the Cosmic Microwave Background, in Astrophysical Journal, vol. 471, 1996, pp. 30–51, DOI:10.1086/177951.
^ WMAP Collaboration, L. Verde, H. V. Peiris, E. Komatsu, M. R. Nolta, C. L. Bennett, M. Halpern, G. Hinshaw e N. Jarosik, First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters, in Astrophysical Journal (Supplement Series), vol. 148, nº 1, 2003, pp. 175–194, DOI:10.1086/377226, arΧiv:astro-ph/0302209.
^ In originale, full width at half maximum
^ Università di Bologna
^ Formazione ed evoluzione delle galassie Archiviato l'11 marzo 2012 in Internet Archive.
^ A. Lewis e A. Challinor, Weak gravitational lensing of the CMB, in Physics Reports, vol. 429, 2006, pp. 1–65, DOI:10.1016/j.physrep.2006.03.002, arΧiv:astro-ph/0601594.
^ Esa, su esa.int.
^ Max Tegmark, L'iniverso matematico, Bollati Boringhieri, 2014.
^ Riccardo Scarpa, E se la radiazione di fondo fosse solo un localismo? Archiviato il 4 marzo 2016 in Internet Archive., Coelum, 170
^ J.V. Narlikar et al., Cosmic iron whiskers: their origin, length distribution and astrophysical consequences Archiviato l'8 dicembre 2015 in Internet Archive.
^ A. Kogut et al., Dipole Anisotropy in the COBE Differential Microwave Radiometers First-Year Sky Maps, in Astrophysical Journal, vol. 419, 1993, pp. 1–6, DOI:10.1086/173453, arΧiv:astro-ph/9312056.
^ APOD: 2009 September 6 - CMBR Dipole: Speeding Through the Universe
^ K. T. Inoue e J. Silk, Local Voids as the Origin of Large-Angle Cosmic Microwave Background Anomalies: The Effect of a Cosmological Constant, in Astrophysical Journal, vol. 664, nº 2, 2007, pp. 650–659, DOI:10.1086/517603, arΧiv:astro-ph/0612347.
^ G. Rossmanith et al., 2009, Non-Gaussian Signatures in the five-year WMAP data as identified with isotropic scaling indices arΧiv:0905.2854
^ ab R. E. Schild, C. H. Gibson, 2008, Goodness in the Axis of Evil arΧiv:0802.3229
^ A. Bernui et al., 2005, Mapping the large-scale anisotropy in the WMAP data arΧiv:astro-ph/0511666
^ T. R. Jaffe et al., 2005, Evidence of vorticity and shear at large angular scales in the WMAP data: a violation of cosmological isotropy?arΧiv:astro-ph/0503213
^
A. de Oliveira-Costa et al., The significance of the largest scale CMB fluctuations in WMAP, in Physical Review D, vol. 69, 2004, p. 063516, DOI:10.1103/PhysRevD.69.063516, arΧiv:astro-ph/0307282.
^ D. J. Schwarz, et al,, Is the low-l microwave background cosmic?, in Physical Review Letters, vol. 93, 2004, p. 221301, DOI:10.1103/PhysRevLett.93.221301, arΧiv:astro-ph/0403353.
^
P. Bielewicz, K. M. Gorski, Low-order multipole maps of CMB anisotropy derived from WMAP, in Monthly Notices of the Royal Astronomical Society, vol. 355, 2004, p. 1283, DOI:10.1111/j.1365-2966.2004.08405.x, arΧiv:astro-ph/0405007.
^ In originale, axis of evil
^
M. Tegmark, A. de Oliveira-Costa e A. Hamilton, A high resolution foreground cleaned CMB map from WMAP, in Physical Review D, vol. 68, 2003, p. 123523, DOI:10.1103/PhysRevD.68.123523, arΧiv:astro-ph/0302496. This paper states, "Not surprisingly, the two most contaminated multipoles are [the quadrupole and octopole], which most closely trace the galactic plane morphology."
^ I. O'Dwyer et al., Bayesian Power Spectrum Analysis of the First-Year Wilkinson Microwave Anisotropy Probe Data, in Astrophysical Journal Letters, vol. 617, 2004, pp. L99–L102, DOI:10.1086/427386, arΧiv:astro-ph/0407027.
^
A. Slosar, U. Seljak, Assessing the effects of foregrounds and sky removal in WMAP, in Physical Review D, vol. 70, 2004, p. 083002, DOI:10.1103/PhysRevD.70.083002, arΧiv:astro-ph/0404567.
^ P. Bielewicz et al., Multipole vector anomalies in the first-year WMAP data: a cut-sky analysis, in Astrophysical Journal, vol. 635, 2005, pp. 750–60, DOI:10.1086/497263, arΧiv:astro-ph/0507186.
^ C.J. Copi et al., On the large-angle anomalies of the microwave sky, in Monthly Notices of the Royal Astronomical Society, vol. 367, 2006, pp. 79–102, DOI:10.1111/j.1365-2966.2005.09980.x, arΧiv:astro-ph/0508047.
^
A. de Oliveira-Costa e M. Tegmark, CMB multipole measurements in the presence of foregrounds, in Physical Review D, vol. 74, 2006, p. 023005, DOI:10.1103/PhysRevD.74.023005, arΧiv:astro-ph/0603369.
Altri progetti |
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su radiazione cosmica di fondo
Wikimedia Commons contiene immagini o altri file su radiazione cosmica di fondo
Collegamenti esterni |
- (EN) NASA, CMB Experiments. Lista degli esperimenti sulla CMB dal sito nasa.gov, su lambda.gsfc.nasa.gov. URL consultato il 7 giugno 2012 (archiviato dall'url originale il 16 giugno 2012).
- Roberto Decarli, Il fondo cosmico a microonde (PPT), Osservatorio astronomico di Brera, 2004-2005. URL consultato il 30 giugno 2010 (archiviato dall'url originale il 9 dicembre 2012).
- (EN) La radiazione di fondo su arxiv.org, su xstructure.inr.ac.ru. URL consultato il 30 giugno 2010.
- (EN) Fraser Cain e Dr. Pamela Gay: intervista sul Big Bang e la radiazione cosmica di fondo, su astronomycast.com, 30 giugno 2010 (archiviato dall'url originale il 26 giugno 2010 Il valore del parametro
dataarchivionon combacia con la data decodificata dall'URL: 4 giugno 2012 (aiuto)).
.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}


