Monopolo magnetico
| Monopolo magnetico | |
|---|---|
 Paul Dirac ha proposto l'esistenza di una particella con carica magnetica netta per spiegare il valore della carica elettrica del protone e dell'elettrone | |
| Composizione | Particella elementare |
| Interazione | gravitazionale, elettromagnetica |
| Status | particella ipotetica |
| Teorizzata | Paul Dirac (1931) |
| Simbolo | M |
| Massa | superiore a 360 GeV |
In elettromagnetismo un monopolo magnetico è un'ipotetica particella prevista da alcuni modelli teorici, la cui esistenza non è mai stata verificata sperimentalmente, costituita da un solo polo magnetico e caratterizzata quindi dal possedere una carica magnetica netta.[1][2]
Nel 1931 Paul Dirac sviluppò un grande interesse verso queste particelle dimostrando che l'eventuale esistenza dei monopoli magnetici è legata ai fenomeni di quantizzazione della carica elettrica.[3] Gli interessi moderni della fisica moderna verso questo concetto provengono dalla teoria della grande unificazione e dalla teoria delle superstringhe.[4][5]
L'unità del SI proposta per la carica magnetica è il Wb (già in uso come unità di misura del flusso magnetico), sebbene siano possibili differenti convenzioni, come ad esempio l'A·m.
Indice
1 Storia
2 Descrizione
2.1 Equazioni di Maxwell con monopoli magnetici
2.2 Quantizzazione della carica elettrica
3 Interpretazione topologica
3.1 Stringhe di Dirac
3.2 Teoria delle stringhe
3.3 Formulazione matematica
4 Teoria della grande unificazione
5 Ricerche sperimentali
6 Monopoli nei sistemi della materia condensata
7 Note
8 Bibliografia
9 Voci correlate
10 Collegamenti esterni
Storia |

Pierre Curie è stato il primo a proporre l'esistenza di una particella con carica magnetica netta
Nella teoria classica la carica magnetica è antica quanto le equazioni di Maxwell. Per decenni i monopoli magnetici sono stati largamente considerati finzioni teoriche risultanti da certi meri calcoli matematici. Il primo ad ipotizzare l'esistenza di una particella con queste caratteristiche fu Pierre Curie nel 1894[6]. Dirac, nel 1931, mostrò che l'esistenza di un monopolo magnetico potrebbe spiegare la quantizzazione della carica elettrica. L'elettrone e il protone hanno infatti cariche elettriche perfettamente identiche in modulo ma opposte in segno. Tuttavia queste due particelle hanno caratteristiche completamente differenti fra di loro, ad esempio il protone è circa duemila volte più massivo dell'elettrone, per cui risulta sorprendente l'identità a meno del segno della loro carica elettrica.[7] Riguardo ai monopoli magnetici, Dirac scrisse:
.mw-parser-output .citazione-table{margin-bottom:.5em;font-size:95%}.mw-parser-output .citazione-table td{padding:0 1.2em 0 2.4em}.mw-parser-output .citazione-lang{vertical-align:top}.mw-parser-output .citazione-lang td{width:50%}.mw-parser-output .citazione-lang td:first-child{padding:0 0 0 2.4em}.mw-parser-output .citazione-lang td:nth-child(2){padding:0 1.2em}
| (EN) «One would be surprised if Nature had made no use of it.» | (IT) «Uno sarebbe sorpreso se la natura non ne avesse fatto uso» |
| (Paul Adrien Maurice Dirac[3]) |
Dirac dimostrò che se esiste un monopolo magnetico la sua carica magnetica deve essere quantizzata e deve valere un numero intero di volte la costante di Planck divisa la carica elementare.[3]
Da queste prime considerazioni teoriche sono state svolte sistematiche ricerche sperimentali dei monopoli. Esperimenti nel 1975 e 1982[8][9] produssero eventi che vennero inizialmente ricondotti ai monopoli magnetici, ma che poi non sono stati considerati come conclusivi. Resta perciò la possibilità che i monopoli non esistano affatto.
Nonostante la mancanza di evidenze sperimentali l'esistenza dei monopoli magnetici è considerata come una questione aperta. Il moderno approccio teorico alle particelle fisiche, in particolare la Teoria della grande unificazione e la teoria delle superstringhe, predicono l'esistenza di monopoli nell'universo. Infatti Joseph Polchinski, un noto fisico teorico delle stringhe, descrive l'esistenza dei monopoli come "una delle scommesse più sicure che uno possa fare circa la fisica non ancora scoperta".[10] Queste teorie non sono necessariamente in contrasto con le evidenze sperimentali: infatti, alcuni modelli proposti suggeriscono che i monopoli magnetici esistano, ma che è improbabile osservarli, essendo entrambi troppo massivi per essere generati negli acceleratori di particelle e troppo rari nell'universo per essere osservati dai rivelatori di particelle.
A partire dal 2009 la ricerca si è concentrata anche sulla possibilità di costruire "artificialmente" dei monopoli magnetici, cioè di realizzare eccitazioni nella materia ordinaria che si comportano effettivamente come dei monopoli magnetici.[7][11] Queste scoperte si riferiscono a fenomeni in materiali cristallini vicini allo zero assoluto, ma non sono correlate alla verifica dell'esistenza di particelle isolate dotate di una carica magnetica netta. Sono piuttosto dei tubi di flusso che formano un dipolo magnetico: in questi, sotto determinate condizioni, può accadere che i due monopoli possono muoversi in modo indipendente ed essere considerati quindi delle quasi-particelle (vedi sotto monopoli nei sistemi della materia condensata). Tramite il decadimento di muoni è stata anche scoperta la magnetricità[12], ossia l'equivalente magnetico della corrente elettrica.
Nel 2014 David S. Hall, dell'Amherst College, in Massachusetts, col suo team ha rilevato sperimentalmente i monopoli magnetici tramite la polarizzazione di atomi di rubidio tenuti ad una temperatura vicina allo zero assoluto[13].
Descrizione |
.mw-parser-output .vedi-anche{border:1px solid #CCC;font-size:95%;margin-bottom:.5em}.mw-parser-output .vedi-anche td:first-child{padding:0 .5em}.mw-parser-output .vedi-anche td:last-child{width:100%}
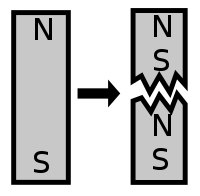
È impossibile creare un monopolo magnetico da una barra magnetica. Se la barra magnetica è tagliata a metà, non si generano due corpi distinti uno dei quali con il polo nord e l'altro con il polo sud. Piuttosto, ciascuna parte avrà il suo polo nord e il suo polo sud. Un monopolo magnetico non può essere creato dalla materia come atomi o elettroni, ma sarebbe piuttosto una nuova particella elementare.
I magneti interagiscono fra di loro, similmente a quanto accade alle cariche elettriche. I poli simili si respingono e i poli diversi si attraggono. Quando un magnete (un oggetto descritto convenzionalmente come composto da due poli magnetici nord e sud) è tagliato a metà lungo l'asse che unisce i due poli, le parti risultanti sono due normali magneti più piccoli. Ciascuno ha il proprio polo Nord e Sud.[14]
Il moto degli elettroni genera negli atomi campi magnetici molto piccoli. Nel modello atomico di Bohr gli elettroni orbitano intorno al nucleo. La loro rotazione costante è paragonabile teoricamente a una piccola spira percorsa da corrente che induce quindi un campo magnetico secondo la legge di Biot-Savart.[15]

Nella figura in alto è mostrato il campo elettrico di dipolo generato da una carica elettrica positiva e una negativa. In basso a sinistra è invece mostrato il campo magnetico assolutamente simile generato da una coppia di monopoli magnetici di carica opposta, con le linee di campo che partono dalla carica "Nord" e finiscono a quella "Sud". In basso a destra è invece mostrato il campo magnetico di un ordinario magnete, con le linee di campo che si avvolgono circolarmente senza né pozzi né sorgenti.
I magneti permanenti hanno campi magnetici misurabili perché gli atomi e le molecole sono organizzate in modo che tutti i loro diversi momenti magnetici sono coerentemente allineati, sommandosi per formare un unico grande campo aggregato.[16] In questo modello la mancanza di singolo polo ha un significato intuitivo; il taglio del magnete a metà non ha alcun effetto sulla disposizione delle molecole all'interno di esso. Il risultato finale è due barre magnetiche in cui gli atomi hanno lo stesso orientamento di prima e quindi generano un campo magnetico con lo stesso orientamento del magnete originale più grande. È quindi impossibile separare il polo nord di un magnete da quello sud e realizzare in questo modo un monopolo magnetico.
Un monopolo magnetico è piuttosto una nuova particella elementare diversa da quelle che si possono trovare nella materia ordinaria e che può esistere anche in forma libera nello spazio vuoto dell'universo.[14]
Un monopolo magnetico in un campo magnetico viene accelerato esattamente come una carica elettrica in un campo elettrico. Come la particella carica acquista energia cinetica a spese del campo elettrico, nella stessa maniera un monopolo magnetico acquisterebbe energia cinetica a spese del campo magnetico. Nello spazio intergalattico è presente un campo magnetico e questo pone un limite al numero dei monopoli magnetici esistenti noto come limite di Parker.[17]
Equazioni di Maxwell con monopoli magnetici |
Le equazioni di Maxwell dell'elettromagnetismo collegano i campi magnetici e elettrici alla presenza e ai movimenti delle cariche elettriche. La forma standard delle equazioni prevede una carica elettrica, ma non presuppone una carica magnetica. Le equazioni di Maxwell tuttavia si semplificano quando tutte le cariche elettriche sono nulle e in questo modo è possibile ricavare l'equazione di un'onda. In questa situazione le equazioni sono simmetriche rispetto allo scambio del campo elettrico con quello magnetico.
Equazioni completamente simmetriche possono essere scritte anche nella situazione più generale, se si tiene conto della possibilità di cariche magnetiche dal comportamento analogo alle cariche elettriche. Con l'aggiunta della densità di carica magnetica, detta ρH{displaystyle rho _{H}}

Nome
Senza Monopoli Magnetici
Con Monopoli Magnetici
Legge di Gauss elettrica
∇⋅E=4πρE{displaystyle nabla cdot mathbf {E} =4pi rho _{E}}
∇⋅E=4πρE{displaystyle nabla cdot mathbf {E} =4pi rho _{E}}
Legge di Gauss magnetica
∇⋅B=0{displaystyle nabla cdot mathbf {B} =0}
∇⋅B=4πρH{displaystyle nabla cdot mathbf {B} =4pi rho _{H}}
Legge di Faraday-Neumann
−∇×E=1c∂B∂t{displaystyle -nabla times mathbf {E} ={frac {1}{c}}{frac {partial mathbf {B} }{partial t}}}
−∇×E=1c∂B∂t+4πcJH{displaystyle -nabla times mathbf {E} ={frac {1}{c}}{frac {partial mathbf {B} }{partial t}}+{frac {4pi }{c}}mathbf {J} _{H}}
Teorema di Ampère-Maxwell
∇×B=1c∂E∂t+4πcJE{displaystyle nabla times mathbf {B} ={frac {1}{c}}{frac {partial mathbf {E} }{partial t}}+{frac {4pi }{c}}mathbf {J} _{E}}
∇×B=1c∂E∂t+4πcJE{displaystyle nabla times mathbf {B} ={frac {1}{c}}{frac {partial mathbf {E} }{partial t}}+{frac {4pi }{c}}mathbf {J} _{E}}
Note: Per le equazioni in forma non normalizzata, rimuovere il fattore c.
Anche la forza di Lorentz diviene simmetrica:
F=qE(E+vc×B)+qB(B−vc×E){displaystyle mathbf {F} =q_{E}left(mathbf {E} +{frac {mathbf {v} }{c}}times mathbf {B} right)+q_{B}left(mathbf {B} -{frac {mathbf {v} }{c}}times mathbf {E} right)}.
Nelle unità del Sistema Internazionale invece ci sono due convenzioni differenti per la definizione della carica magnetica. Nella prima, l'unità di misura proposta per la carica magnetica è il weber[18], che è già presente come unità di misura del flusso magnetico, mentre nell'altra, la carica magnetica ha le unità di ampere-metro.
Le equazioni di Maxwell allora assumono la seguente forma:
| Nome | Senza monopoli magnetici | Convenzione Ampere·metro | Convenzione Weber |
|---|---|---|---|
| Legge di Gauss elettrica | ∇⋅E=ρEε{displaystyle nabla cdot mathbf {E} ={frac {rho _{E}}{varepsilon }}}  | ∇⋅E=ρEε{displaystyle nabla cdot mathbf {E} ={frac {rho _{E}}{varepsilon }}} | ∇⋅E=ρEε{displaystyle nabla cdot mathbf {E} ={frac {rho _{E}}{varepsilon }}}  |
| Legge di Gauss magnetica | ∇⋅B=0{displaystyle nabla cdot mathbf {B} =0}  | ∇⋅B=μρH{displaystyle nabla cdot mathbf {B} =mu rho _{H}} | ∇⋅B=ρH{displaystyle nabla cdot mathbf {B} =rho _{H}}  |
| Legge di Faraday-Neumann | −∇×E=∂B∂t{displaystyle -nabla times mathbf {E} ={frac {partial mathbf {B} }{partial t}}}  | −∇×E=∂B∂t+μJH{displaystyle -nabla times mathbf {E} ={frac {partial mathbf {B} }{partial t}}+mu mathbf {J} _{H}} | −∇×E=∂B∂t+JH{displaystyle -nabla times mathbf {E} ={frac {partial mathbf {B} }{partial t}}+mathbf {J} _{H}}  |
| Teorema di Ampère-Maxwell | ∇×B=με∂E∂t+μJE{displaystyle nabla times mathbf {B} =mu varepsilon {frac {partial mathbf {E} }{partial t}}+mu mathbf {J} _{E}}  | ∇×B=με∂E∂t+μJE{displaystyle nabla times mathbf {B} =mu varepsilon {frac {partial mathbf {E} }{partial t}}+mu mathbf {J} _{E}} | ∇×B=με∂E∂t+μJE{displaystyle nabla times mathbf {B} =mu varepsilon {frac {partial mathbf {E} }{partial t}}+mu mathbf {J} _{E}}  |
| Forza di Lorentz | F=qE(E+v×B){displaystyle mathbf {F} =q_{E}left(mathbf {E} +mathbf {v} times mathbf {B} right)}  | F=qE(E+v×B)+qB(B−v×Ec2){displaystyle mathbf {F} =q_{E}left(mathbf {E} +mathbf {v} times mathbf {B} right)+q_{B}left(mathbf {B} -mathbf {v} times {frac {mathbf {E} }{c^{2}}}right)} | F=qE(E+v×B)+qBμ(B−v×Ec2){displaystyle mathbf {F} =q_{E}left(mathbf {E} +mathbf {v} times mathbf {B} right)+{frac {q_{B}}{mu }}left(mathbf {B} -mathbf {v} times {frac {mathbf {E} }{c^{2}}}right)}  |
In tutte queste equazioni ρH è la densità di carica magnetica, Jm è la densità di corrente magnetica, e qH è la carica magnetica di una particella di test, definite analogamente alle rispettive cariche e densità elettriche.
Se le cariche magnetiche non esistono, o se esistono ma sono assenti nella regione presa in considerazione, le nuove variabili sono nulle e le equazioni estese si riducono alle equazioni convenzionali dell'elettromagnetismo come ∇⋅B=0{displaystyle nabla cdot mathbf {B} =0}
Quantizzazione della carica elettrica |
La quantizzazione della carica elettrica venne derivata teoricamente da Paul Dirac a partire dalla meccanica quantistica in un suo lavoro sull'elettromagnetismo quantistico. Senza i monopoli magnetici, la presenza di cariche elettriche discrete deve essere semplicemente inserita nelle equazioni, ma nel 1931 Dirac osservò che una carica discreta discende naturalmente dalla meccanica quantistica.[3]
Il risultato di Dirac può essere ottenuto con un ragionamento semiclassico. Un monopolo statico dovrebbe generare un campo magnetico radiale simile a quello elettrico:[19]
- B=qB4πr2u^r{displaystyle mathbf {B} ={frac {q_{B}}{4pi r^{2}}}{hat {mathbf {u} }}_{r}}
Tuttavia, al contrario del campo elettrostatico, il momento angolare L{displaystyle mathbf {L} }
- dLdt=ddt(mr×drdt)=r×md2rdt2{displaystyle {frac {dmathbf {L} }{dt}}={frac {d}{dt}}left(mmathbf {r} times {frac {dmathbf {r} }{dt}}right)=mathbf {r} times m{frac {d^{2}mathbf {r} }{dt^{2}}}}
e usando l'espressione della forza di Lorentz:
- F=md2rdt2=qEv×B=qEdrdt×B{displaystyle mathbf {F} =m{frac {d^{2}mathbf {r} }{dt^{2}}}=q_{E}mathbf {v} times mathbf {B} =q_{E}{frac {dmathbf {r} }{dt}}times mathbf {B} }
si ha infatti:
- dLdt=qBqE4πr×(drdt×1r2ur)=qBqE4π(1rdrdt−urr2(drdt⋅r))=qBqE4πdurdt{displaystyle {frac {dmathbf {L} }{dt}}={frac {q_{B}q_{E}}{4pi }}mathbf {r} times left({frac {dmathbf {r} }{dt}}times {frac {1}{r^{2}}}mathbf {u} _{r}right)={frac {q_{B}q_{E}}{4pi }}left({frac {1}{r}}{frac {dmathbf {r} }{dt}}-{frac {mathbf {u} _{r}}{r^{2}}}left({frac {dmathbf {r} }{dt}}cdot mathbf {r} right)right)={frac {q_{B}q_{E}}{4pi }}{frac {dmathbf {u} _{r}}{dt}}}
Dell'espressione esplicita si nota che ad essere conservato non è il momento angolare classico L{displaystyle mathbf {L} }
- Lt=L−qBqE4πur{displaystyle mathbf {L_{t}} =mathbf {L} -{frac {q_{B}q_{E}}{4pi }}mathbf {u} _{r}}
L'ultimo termine aggiunto può essere interpretato come il momento angolare trasportato dal campo elettromagnetico, dato classicamente dal prodotto del vettore posizione r{displaystyle mathbf {r} }

- qBqE4πz=nzℏ2{displaystyle {frac {q_{B}q_{E}}{4pi }}mathbf {z} =n_{z}{frac {hbar }{2}}}
dove nz=(±1,±2,±3,...){displaystyle n_{z}=(pm 1,pm 2,pm 3,...)}

- qE=nz2πℏqB=(±e,±2e,±3e,...){displaystyle q_{E}=n_{z}{frac {2pi hbar }{q_{B}}}=(pm e,pm 2e,pm 3e,...)}
in accordo con quanto osservato nella natura. Dirac derivò questa relazione non ricorrendo ad un ragionamento semiclassico come quello presentato, ma piuttosto usando le proprietà delle trasformazioni di gauge applicate alla funzione d'onda.
Interpretazione topologica |
Stringhe di Dirac |
Una carica magnetica netta e statica introduce un campo magnetico analogo a quello elettrostatico:[21]
- B=qB4π1r2ur{displaystyle mathbf {B} ={frac {q_{B}}{4pi }}{frac {1}{r^{2}}}mathbf {u} _{r}}
Un campo magnetico centrale di questo tipo ha tuttavia una divergenza non nulla nell'origine x=0{displaystyle mathbf {x} =0}
- ∇⋅B=qBδ3(x){displaystyle nabla cdot mathbf {B} =q_{B}delta ^{3}(mathbf {x} )}
e diviene impossibile introdurre un potenziale vettore A{displaystyle mathbf {A} }

- ∇⋅B=∇⋅(∇×A)=0{displaystyle nabla cdot mathbf {B} =nabla cdot (nabla times mathbf {A} )=0}
I potenziali vettori tuttavia hanno una grande importanza nella formulazione quantistica del campo elettromagnetico e dell'interazione fra questo e le particelle cariche, per cui è difficile evitare di costruire un potenziale vettore A{displaystyle mathbf {A} }
A questo scopo si può notare che un campo vettore A+{displaystyle mathbf {A} ^{+}}
- A+=Aϕ+uϕ=qB4π1−cos(θ)rsin(θ)uϕ{displaystyle mathbf {A} ^{+}=A_{phi }^{+}mathbf {u} _{phi }={frac {q_{B}}{4pi }}{frac {1-cos(theta )}{rsin(theta )}}mathbf {u} _{phi }}
permette di realizzare un campo magnetico centrale:
- ∇×A+=1rsin(θ)∂∂θ(sin(θ)Aϕ)ur−1r∂∂r(rAϕ)uθ=qB4π1r2ur{displaystyle nabla times mathbf {A} ^{+}={frac {1}{rsin(theta )}}{frac {partial }{partial theta }}left(sin(theta )A_{phi }right)mathbf {u} _{r}-{frac {1}{r}}{frac {partial }{partial r}}left(rA_{phi }right)mathbf {u} _{theta }={frac {q_{B}}{4pi }}{frac {1}{r^{2}}}mathbf {u} _{r}}
ma è inevitabilmente singolare ed infinito per θ=π{displaystyle theta =pi }



- A−=Aϕ−uϕ=qB4π−1−cos(θ)rsin(θ)uϕ{displaystyle mathbf {A} ^{-}=A_{phi }^{-}mathbf {u} _{phi }={frac {q_{B}}{4pi }}{frac {-1-cos(theta )}{rsin(theta )}}mathbf {u} _{phi }}
singolare questa volta lungo l'asse-z positivo per θ=0{displaystyle theta =0}
- A+−A−=2qB4πuϕrsin(θ)=2qB4π∇ϕ{displaystyle mathbf {A} ^{+}-mathbf {A} ^{-}={frac {2q_{B}}{4pi }}{frac {u_{phi }}{rsin(theta )}}={frac {2q_{B}}{4pi }}nabla phi }
classicamente è possibile usare i due potenziali intercambiabilmente senza modificare la fisica dei campi elettromagnetici generati. È quindi possibile scegliere il potenziale vettore A+{displaystyle mathbf {A} ^{+}}







- A(r,θ,ϕ)={A+0≤θ<π−εA−0+ε<θ≤π{displaystyle mathbf {A} (r,theta ,phi )={begin{cases}mathbf {A} ^{+}&0leq theta <pi -varepsilon \mathbf {A} ^{-}&0+varepsilon <theta leq pi end{cases}}}
Tuttavia dal punto di vista quantistico una trasformazione di gauge del campo vettore si riflette in un cambiamento simultaneo della fase della funzione d'onda Ψ(r,θ,ϕ){displaystyle Psi (r,theta ,phi )}
- Ψ′(r,θ,ϕ)→exp(iqEqBℏϕ)Ψ(r,θ,ϕ){displaystyle Psi '(r,theta ,phi )rightarrow exp left(i{frac {q_{E}q_{B}}{hbar }}phi right)Psi (r,theta ,phi )}
La funzione d'onda tuttavia deve essere continua e monodroma, Ψ′(r,θ,ϕ)=Ψ′(r,θ,ϕ+2π){displaystyle Psi '(r,theta ,phi )=Psi '(r,theta ,phi +2pi )}
- qEqBℏ=2πn{displaystyle {frac {q_{E}q_{B}}{hbar }}=2pi n}
con n{displaystyle n}
Una teoria di gauge come l'elettromagnetismo è definita da un campo di gauge, con associato un elemento del gruppo per ogni curva nello spazio tempo. Per curve infinitesime, l'elemento del gruppo è circa uguale all'identità, mentre per curve lunghe l'elemento del gruppo è il prodotto successivo di elementi infinitesimi lungo il percorso. Nell'elettrodinamica, il gruppo è U(1), che è il gruppo dei numeri complessi unimodulari rispetto alla moltiplicazione. Per linee infinitesime, l'elemento del gruppo è 1+iAμdxμ{displaystyle 1+iA_{mu }dx^{mu }}
- ∏s(1+ieAμdxμdsds)=eie∫A⋅dx.{displaystyle prod _{s}(1+ieA_{mu }{operatorname {d} x^{mu } over operatorname {d} s}operatorname {d} s)=mathrm {e} ^{ieint Acdot operatorname {d} x}.}
- ∏s(1+ieAμdxμdsds)=eie∫A⋅dx.{displaystyle prod _{s}(1+ieA_{mu }{operatorname {d} x^{mu } over operatorname {d} s}operatorname {d} s)=mathrm {e} ^{ieint Acdot operatorname {d} x}.}
La mappa che associa alla curva il suo rispettivo elemento del gruppo è chiamata olonomia, e per il gruppo di gauge U(1) questa è il fattore di fase che la funzione d'onda delle particelle cariche acquisisce percorrendo per intero il circuito. Per un circuito:
- e∮∂DA⋅dx=e∫D(∇×A)dS=e∫DBdS.{displaystyle eoint _{partial D}Acdot dx=eint _{D}(nabla times A)dS=eint _{D}B,dS.}
Quindi questa è la fase geometrica acquisita da una particella carica quando in un circuito vi è un flusso magnetico non nullo, ed essa prende il nome di fase di Berry. Quando un piccolo solenoide ha un flusso magnetico netto, vi sono delle frange di interferenza per le particelle cariche che circolano lungo o intorno al solenoide, che rivela così la sua presenza. Queste frange di interferenza sono state verificate sperimentalmente e questo fenomeno è noto come effetto di Aharonov-Bohm.
Ma se tutte le particelle cariche sono multipli interi di e, solenoidi con un flusso di 2π/e{displaystyle 2pi /e}


Un campo magnetico centrale di un monopolo può infatti essere generato da un solenoide estremamente sottile, in cui una delle due estremità è posta all'infinito. All'interno del solenoide estremamente sottile il potenziale vettore A→{displaystyle {vec {A}}}
La soluzione dei monopoli di Dirac infatti descrive un solenoide fatto come una linea infinitesima che finisce in un punto, e l'esatta locazione del solenoide è la parte singolare della soluzione, la stringa di Dirac. Le stringhe di Dirac collegano monopoli ed antimonopoli di opposte cariche magnetiche, anche se nella versione di Dirac, la stringa termina all'infinito. La stringa è invisibile, in modo che si può metterla dovunque e dividendo lo spazio in due zone, il campo in ogni zona può essere reso non singolare facendo scorrere la stringa dove non può essere veduta.
Teoria delle stringhe |
Alcuni fisici teorici pensano che il nostro universo sia modellato dalla gravità quantistica. Quando si tiene conto della gravità, la singolarità monopolare può essere un buco nero, e per grandi masse e cariche magnetiche, la massa del buco nero è equivalente alla carica del buco nero, quindi la massa dei buchi neri magnetici non è infinita. Se il buco nero decade completamente per emissione della radiazione di Hawking, come richiesto dal principio olografico, le particelle cariche non possono essere troppo pesanti. I monopoli dovrebbero avere una massa più piccola o comparabile alla loro carica in unità naturali.
Quindi per la teoria olografica, e la teoria delle stringhe è l'unico esempio noto, ci sono sempre monopoli di massa finita. Per l'ordinario elettromagnetismo, il limite della massa non è molto importante perché riguarda la massa di Planck.
Formulazione matematica |
In matematica un campo di gauge è definito come la connessione sopra un fibrato principale nello spazio-tempo. G è un gruppo di gauge e agisce su ciascuna fibra del fibrato separatamente.
Una connessione su un fibrato G ci dice come incollare le fibre F fra loro nell'intorno di un punto M. Inizia con un gruppo di simmetria continuo G che agisce su F, e poi associa un elemento del gruppo con ciascun cammino infinitesimo. La moltiplicazione del gruppo lungo ciascun cammino ci dice come muoverci da un punto del fibrato ad un altro, dall'azione dell'elemento di G di un cammino sulla fibra F.
In matematica la definizione di fibrato è fatta in modo da sottolineare la topologia, in modo che la nozione di connessione sia aggiunta sopra come una ulteriore proprietà successiva. In fisica, la connessione è un oggetto fisico fondamentale. Una volta che si ha la connessione, appaiono fibrati non banali che si verificano come connessioni di fibrati banali. Per esempio il toro aggrovigliato è la connessione su un fibrato U(1) di un cerchio su un cerchio.
Se lo spazio-tempo non ha topologia, se è R4 lo spazio di tutte le possibili connessioni di G-fibrati principali è uno spazio connesso. Ma, se si considera cosa succede quando si rimuove una linea d'universo di tipo tempo dallo spazio-tempo, il risultante spazio tempo è omotopicamente equivalente alla sfera topologica S2.
Un G-fibrato principale su S2 è definito ricoprendo S2 con due carte, ciascuna delle quali è omeomorfa alla 2-palla aperta in modo che la loro intersezione è omeomorfa alla striscia S1×I. Le 2-palle sono omotopicamente banali e la linea è omotopicamente equivalente al cerchio S1. Quindi una classificazione topologica delle possibili connessioni è ridotta a classificare le loro funzioni di transizione. Le funzioni di transizione mappano la striscia in G, e le differenti vie di mappare una striscia in G è data dal primo gruppo di omotopia di G.
Quindi, nella formulazione dei G-fibrati principali, una teoria di gauge ammette monopoli di Dirac garantendo che G non è semplicemente connesso, quindi ci sono cammini che vanno intorno al gruppo che non possono essere deformati ad un punto. U(1), che ha la carica quantizzata, non è semplicemente connesso e può avere monopoli di Dirac, mentre R, il suo gruppo di ricoprimento universale, è semplicemente connesso e non ha cariche quantizzate e non ammette monopoli di Dirac. La definizione matematica è equivalente a quella fisica, in modo che, seguendo Dirac, sono ammessi i campo di gauge i quali sono solo definiti a coppie di cammini e il campo di gauge su differenti cammini sono incollati dopo una trasformazione di gauge.
Questo argomento per i monopoli è una ridefinizione dei precedenti argomenti per le teorie puramente U(1). È generalizzabile a d + 1 dimensioni con d≥2{displaystyle dgeq 2}
Teoria della grande unificazione |
Negli ultimi decenni una nuova classe di teorie in fisica teorica ha anche supposto la presenza di monopoli magnetici.
Agli inizi degli anni '70 i successi della teoria quantistica dei campi e di quella di gauge nell'unificazione della forza elettrodebole con quella nucleare forte ha spinto molti teorici nel tentativo di combinare fra loro l'elettromagnetismo e le forze nucleari in una teoria detta GUT, Teoria della grande unificazione. Molti modelli sono stati proposti, molti dei quali hanno curiosi aspetti che suggeriscono la presenza di reali monopoli magnetici. Più precisamente la GUT predice un range di particelle note come dioni, che allo stato fondamentale sono dei monopoli. La carica dei monopoli predetta dalla GUT è di circa 1 o 2 gD, variando a seconda del modello.
La maggior parte delle particelle apparse in un campo quantistico sono instabili e decadono in altre particelle secondo varie reazioni che conservano determinate quantità. Le particelle stabili sono tali poiché non ci sono particelle più leggere e stabili in cui decadere conservando queste quantità. Per esempio l'elettrone ha un numero leptonico di 1 e una carica elettrica unitaria negativa e l'ovvia stabilità dell'elettrone è garantita dal fatto che non ci sono particelle più leggere che conservino questi valori. Al contrario il muone, una sorta di pesante elettrone, decade in questi ultimi e non è stabile.
Anche i dioni nella GUT sono stabili, ma per ragioni completamente differenti. I dioni sono previsti in conseguenza della rottura della simmetria avvenuta nei primi istanti di vita dell'universo. In questo modello, i dioni sono presenti nella configurazione di vuoto in una particolare area dell'universo, in accordo con l'originale teoria di Dirac. Questi rimangono stabili, non in seguito alle condizioni di conservazione, ma perché non ci sono stati topologici più elementari nei quali possano decadere.
La lunghezza di scala a cui queste configurazioni possono esistere è chiamata "lunghezza di correlazione del sistema". Una lunghezza di correlazione non può essere più larga di quanto concesso dal principio di causalità; inoltre, la lunghezza di correlazione per poter creare monopoli magnetici deve essere grande al massimo quanto la dimensione dell'orizzonte determinata dall'espansione dell'universo. In accordo con la logica, ci dovrebbe essere al massimo un monopolo per volume di orizzonte come accadeva quando occorse la rottura della simmetria. Questo fornisce una stima diretta dell'ammontare dei monopoli oggi, che dovrebbe essere circa 1011 volte la densità critica del nostro universo. L'universo sembra trovarsi circa nei dintorni della densità critica, quindi i monopoli dovrebbero essere abbastanza comuni. Per questa ragione, i monopoli divennero oggetto di grande interesse negli anni '70 e '80, insieme all'altra previsione della GUT, il decadimento del protone. L'apparente problema con i monopoli è risolto dall'inflazione cosmica che riduce di molto l'attesa abbondanza di monopoli magnetici.
Molte altre particelle predette dalla GUT sono oltre le nostre attuali possibilità sperimentali. Per esempio una grande classe di particelle note come bosoni X e Y sono le particelle previste per mediare la forza elettrodebole, ma queste particelle sono estremamente instabili e massive, negando quindi la possibilità pratica di poterle creare direttamente negli acceleratori di particelle.
Ricerche sperimentali |
Negli anni è stato fatto un grande numero di tentativi di scoprire sperimentalmente l'esistenza dei monopoli magnetici. In uno dei metodi più semplici si usano circuiti chiusi di superconduttori per poter osservare sorgenti magnetiche anche molto deboli, tecnica chiamata "dispositivo superconduttore a interferenza quantistica" ("superconducting quantum interference device", o SQUID). Data una prevista densità i circuiti abbastanza piccoli da potere essere inseriti in laboratorio dovrebbero osservare circa un evento di monopolo all'anno. Sebbene siano stati registrati alcuni eventi promettenti, in particolare l'evento rilevato da Blas Cabrera la notte del 14 febbraio 1982 (data chiamata quindi talvolta "Il giorno dei Monopoli di San Valentino"[22]), non ci sono mai stati eventi riproducibili in merito all'esistenza di monopoli magnetici.[9]
Oltre a queste tecniche si può cercare la presenza dei monopoli negli acceleratori di particelle direttamente o indirettamente. Le ricerche dirette cercano di verificare l'esistenza dei monopoli producendoli nello stato finale di un processo di scattering, come per esempio quello alla Drell-Yan:
- p+p¯→M+M¯+X{displaystyle p+{bar {p}}rightarrow M+{bar {M}}+X}
in cui si considera l'urto di una coppia protone-antiprotone che produce anche una coppia monopolo antimonopolo. Con questo tipo di analisi non si è mai osservato alcun evento di produzione di monopoli magnetici e si è così stabilito che un eventuale monopolo dovrebbe avere massa superiore a 360 GeV[23].
Le ricerche indirette si rivolgono invece a cercare l'esistenza dei monopoli nelle correzioni virtuali radiative a processi che non comportano direttamente la produzione di monopoli magnetici nello stato finale, come ad esempio il decadimento del bosone Z in fotoni. Questi studi hanno stabilito che un monopolo magnetico di spin zero non può avere una massa inferiore a 1220 |m′|{displaystyle |m'|}

Altre ricerche sono state condotte tentando di evidenziare la presenza di monopoli magnetici fra i raggi cosmici. Un importante esperimento di questo tipo è stato condotto nei laboratori nazionali del Gran Sasso ed è stato chiamato con l'acronimo MACRO (Monopole, Astrophysics and Cosmic Ray Observatory). L'esperimento, concluso nel 2001, aveva come obbiettivo la ricerca di monopoli ad alta energia cinetica e con grandi masse che potrebbero essere stati prodotti nei primi istanti di vita dell'universo.[26] Nessun evento associato ai monopoli magnetici è stato rilevato e questo ha permesso di porre il limite superiore di 5.6×10−15 per centimetro quadrato per steradiante per secondo (cm−2sr−1s−1) al flusso cosmico di monopoli con velocità tra un decimillesimo e un millesimo rispetto a quella della luce.[27]
Monopoli nei sistemi della materia condensata |
Mentre un monopolo magnetico come particella non è mai stato osservato, ci sono un grande numero di fenomeni nella fisica della materia condensata dove un materiale, per gli effetti collettivi dei suoi elettroni e ioni, può mostrare effetti emergenti che globalmente hanno proprietà similari con i monopoli magnetici in certi aspetti.[28][29][30][31][32] Questi effetti non devono essere confusi con le particelle 'monopoli magnetici'; in particolare, la divergenza del campo magnetico microscopico è nulla dovunque in questi sistemi, al contrario di quanto accade in presenza di una vera particella 'monopolo magnetico'. L'andamento di queste quasi particelle dovrebbe diventare indistinguibile dai veri monopoli magnetici - e quindi ne meriterebbero appieno il nome - se quelli che sono chiamati tubi di flusso magnetici che connettono questi candidati monopoli divenissero inosservabili, che inoltre significa che questi tubi di flusso dovrebbero essere infinitamente sottili, obbedendo alla regola di quantizzazione di Dirac, e meriterebbero quindi di essere chiamati stringhe di Dirac.
In un articolo pubblicato in Science nel settembre 2009 i ricercatori Jonathan Morris e Alan Tennant dalla Helmholtz-Zentrum Berlin für Materialien und Energie (HZB) insieme con Santiago Grigera dall'Instituto de Física de Líquidos y Sistemas Biológicos (IFLYSIB, CONICET) ed altri colleghi dal Dresden University of Technology, University di St. Andrews e dell'Oxford University hanno descritto l'osservazione di quasi-particelle simili come proprietà ai monopoli. Un singolo cristallo di titanato di disprosio in un reticolo di pirocloro ad alta pressione è stato raffreddato fino a 2 kelvin. Usando lo scattering di neutroni, è stato osservato che il momento magnetico si è allineato allo spin ghiacciato nelle fibre simili ai tubi di flusso intrecciati che assomigliano alle stringhe di Dirac. Al difetto che si è formato alla fine di ogni tubo, il campo magnetico sembra simile a quello di un monopolo. Usando un campo magnetico applicato per rompere la simmetria del sistema, i ricercatori potevano controllare la densità e l'orientamento di queste stringhe. È stato descritto inoltre un contributo alla capacità termica del sistema proveniente da un gas effettivo di queste quasi-particelle.[33][34]
Note |
^ Particle Data Group summary of magnetic monopole search (PDF), su pdg.lbl.gov. URL consultato il 6 marzo 2012.
^ magnetic monopole, su britannica.com. URL consultato il 6 marzo 2012.
^ abcd Paul Dirac, Quantised Singularities in the Electromagnetic Field (PDF), in Proc. Roy. Soc. (London), A 133, 1931, pp. 60-72.
^ Wen, Xiao-Gang; Witten, Edward, Electric and magnetic charges in superstring models,Nuclear Physics B, Volume 261, p. 651-677
^ S. Coleman, The Magnetic Monopole 50 years Later, ristampati in Aspects of Symmetry
^ Pierre Curie, Sur la possibilité d'existence de la conductibilité magnétique et du magnétisme libre (On the possible existence of magnetic conductivity and free magnetism), Séances de la Société Française de Physique (Paris), p76 (1894). (FR) Free access online copy.
^ ab (EN) Artificial Magnetic Monopoles Discovered, su sciencedaily.com. URL consultato il 5 gennaio 2014.
^ P. B. Price, E. K. Shirk; W. Z. Osborne; L. S. Pinsky, Evidence for Detection of a Moving Magnetic Monopole, in Physical Review Letters, vol. 35, 25 agosto 1975, pp. 487-490, DOI:10.1103/PhysRevLett.35.487.
^ ab Blas Cabrera, First Results from a Superconductive Detector for Moving Magnetic Monopoles, in Physical Review Letters, vol. 48, 17 maggio 1982, pp. 1378-1381, DOI:10.1103/PhysRevLett.48.1378.
^ Joseph Polchinski, Monopoles, Duality, and String Theory, arΧiv:hep-th / 0304042.
^ (EN) Magnetic monopoles detected in a real magnet, su helmholtz-berlin.de. URL consultato il 6 gennaio 2013.
^ La magnetricità è realtà, in Punto informatico.
^ M. W. Ray et al., Observation of Dirac monopoles in a synthetic magnetic field, in Nature, vol. 505, gennaio 2014, pp. 657-660, DOI:10.1038/nature12954.
^ ab (EN) Jonathan Morris, The Hunt for the Magnetic Monopole, su spectrum.ieee.org. URL consultato il 5 gennaio 2014.
^ (EN) Origin of Magnetism .mw-parser-output .chiarimento{background:#ffeaea;color:#444444}.mw-parser-output .chiarimento-apice{color:red}
[collegamento interrotto], su gitam.edu. URL consultato il 5 gennaio 2014.
^ (EN) Origin of permanent magnetism, su farside.ph.utexas.edu. URL consultato il 5 gennaio 2014.
^ M. S. Turner, E. N. Parker;T. J. Bogdan, Magnetic monopoles and the survival of galactic magnetic fields, in Phys. Rev. D, vol. 26, 1982, pp. 1296-1305, DOI:10.1103/PhysRevD.26.1296.
^ Per la convenzione dove la carica magnetica ha unità del Weber, vedere Jackson 1999. In particolare per le equazioni di Maxwell, vedere la sezione 6.11, equazione (6.150), pagina 273, e per la forza di Lorentz, vedere pagina 290. Per la convenzione dove la carica magnetica ha unità di ampere-metro, vedere per esempio arXiv:physics/0508099v1, equazione (4).
^ ab (EN) Dirac monopoles, su phy.duke.edu. URL consultato il 12 gennaio 2014.
^ Jackson 1999, sezione 6.11, equazione (6.153), pagina 275
^ Per la trattazione di questa sezione si veda Magnetic Monopoles (PDF), su bolvan.ph.utexas.edu. URL consultato il 26 gennaio 2014.
^ http://www.nature.com/nature/journal/v429/n6987/full/429010a.html
^ (EN) Abulencia, A. et al., Direct Search for Dirac Magnetic Monopoles in pp̅ Collisions at √s=1.96 TeV (abstract), in Phys. Rev. Lett., vol. 96, 26 maggio 2006, DOI:10.1103/PhysRevLett.96.201801. URL consultato il 6 febbraio 2011.
^ (EN) Milton, K. A., Theoretical and Experimental Status of Magnetic Monopoles (abstract), in ArXiv, 22 febbraio 2006, pp. 60–61, DOI:10.1088/0034-4885/69/6/R02. URL consultato il 6 febbraio 2011.
^ (EN) Graf, S., Schäfer, A.; Greiner, W., Mass limit for Dirac-type magnetic monopoles (abstract), in Elsevier Science B.V., vol. 262, 21 marzo 1991, pp. 463–466, DOI:10.1016/0370-2693(91)90623-X. URL consultato il 6 febbraio 2011.
^ Giorgio Giacomelli and Laura Patrizii, MACRO delivers its final word on monopoles, in CERN Courier, 2003.
^ S. Ahlen et al., Search for slowly moving magnetic monopoles with the MACRO detector, in Physical Review Letters, vol. 72, 1994, pp. 608–612, DOI:10.1103/PhysRevLett.72.608.
^ (EN) Zhong, Fang et al., The Anomalous Hall Effect and Magnetic Monopoles in Momentum Space (abstract), in Science, vol. 302, nº 5046, 3 ottobre 2003, pp. 92–95, DOI:10.1126/science.1089408, ISSN 1095-9203. URL consultato il 15 gennaio 2010.
^ (EN) Lauren Schenkman, Making magnetic monopoles, and other exotica, in the lab, Symmetry Breaking, 29 gennaio 2009. URL consultato il 15 gennaio 2010.
^ (EN) Xiao-Liang Qi, Rundong Li, Jiadong Zang, Shou-Cheng Zhang, Inducing a Magnetic Monopole with Topological Surface States (abstract), in Science, vol. 323, nº 5918, 27 febbraio 2009, pp. 1184–1187, DOI:10.1126/science.1167747. URL consultato il 15 gennaio 2010.
^ (EN) C. Castelnovo, Moessner1 R., Sondhi S. L., Magnetic monopoles in spin ice (abstract), in Nature, nº 451, 3 gennaio 2008, pp. 42-45, DOI:10.1038/nature06433. URL consultato il 15 gennaio 2010.
^ (EN) S. T. Bramwell et al., Measurement of the charge and current of magnetic monopoles in spin ice (abstract), in Nature, nº 461, 15 ottobre 2009, pp. 956-959, DOI:10.1038/nature08500. URL consultato il 15 gennaio 2010.
^ (EN) Magnetic Monopoles Detected In A Real Magnet For The First Time, Science Daily, 4 settembre 2009. URL consultato il 15 gennaio 2010.
^ (EN) D. J. P. Morris et al., Dirac Strings and Magnetic Monopoles in Spin Ice Dy2Ti2O7 (abstract), in Science, vol. 326, nº 5951, 16 ottobre 2009, pp. 411-414, DOI:10.1126/science.1178868. URL consultato il 15 gennaio 2010.
Bibliografia |
- (EN) Charles A. Brau, Modern Problems in Classical Electrodynamics, Oxford University Press, 2004, ISBN 0-19-514665-4.
- (EN) John David Jackson, Classical Electrodynamics, 3ª ed., New York, Wiley, 1999, ISBN 0-471-30932-X.
- (EN) Kimball A. Milton, Theoretical and experimental status of magnetic monopoles (abstract), in Reports on Progress in Physics, vol. 69, nº 6, giugno 2006, pp. 1637–1711, DOI:10.1088/0034-4885/69/6/R02. URL consultato il 15 gennaio 2010.
- (EN) Yakov M. Shnir, Magnetic Monopoles, Springer Verlag, 2005, ISBN 3-540-25277-0.
(EN) M. W. Ray, E. Ruokokoski, S. Kandel, M. Möttönen, D. S. Hall, Observation of Dirac monopoles in a synthetic magnetic field, in Nature, vol. 505, nº 7485, 2014, pp. 657–660, DOI:10.1038/nature12954.accessorichiedeurl(aiuto)
Voci correlate |
- Bosoni X e Y
- Teoria della grande unificazione
Collegamenti esterni |
- Ricerca dei monopoli magnetici: l'esperimento MoEDAL pubblica i primi risultati, su infn.it, Istituto nazionale di fisica nucleare, 10 agosto 2016. URL consultato il 9 luglio 2017.
.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}
.mw-parser-output .CdA{border:1px solid #aaa;width:100%;margin:auto;font-size:90%;padding:2px}.mw-parser-output .CdA th{background-color:#ddddff;font-weight:bold;width:20%}
| Controllo di autorità | GND (DE) 4168573-8 |
|---|

























