Jfyhkgu

Przyspieszenie
Rodzaj wielkości	wektorowa
Symbol	a→{displaystyle {vec {a}}}, a{displaystyle mathbf {a} }, a{displaystyle a}
Jednostka SI	m/s2, m·s-2
W podstawowych jednostkach SI	ms2{displaystyle mathrm {frac {m}{s^{2}}} }
Wymiar	LT2{displaystyle mathrm {frac {L}{T^{2}}} }
Multimedia w Wikimedia Commons
Hasło w Wikisłowniku

Przyspieszenie – wektorowa wielkość fizyczna wyrażająca zmianę wektora prędkości w czasie.

Przyspieszenie definiuje się jako pochodną prędkości po czasie, czyli jest szybkością zmiany prędkości. Jeśli przyspieszenie styczne jest skierowane przeciwnie do zwrotu prędkości ruchu, to wartość prędkości w tym ruchu maleje a przyspieszenie to jest nazywane opóźnieniem.

Definicja |

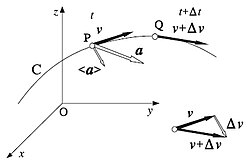
Definicja przyspieszenia

Jeżeli dany wektor r→{displaystyle {vec {r}}} określa położenie punktu materialnego, a wektor v→{displaystyle {vec {v}}} określa prędkość tego punktu, to przyspieszenie a→{displaystyle {vec {a}}} tego punktu jest pochodną prędkości po czasie:

a→=dv→dt{displaystyle {vec {a}}={frac {d{vec {v}}}{dt}}}

Ponieważ prędkość jest pochodną położenia po czasie, to przyspieszenie można zapisać jako drugą pochodną położenia po czasie:

a→=d2r→dt2{displaystyle {vec {a}}={frac {d^{2}{vec {r}}}{dt^{2}}},}

Jednostką przyspieszenia w układzie SI jest metr na sekundę do kwadratu.

[a→]=ms2{displaystyle left[{vec {a}}right]={frac {text{m}}{{text{s}}^{2}}}}

Związek z dynamiką |

Zgodnie z drugą zasadą dynamiki przyspieszenie ciała jest proporcjonalne do wypadkowej siły F działającej na to ciało i odwrotnie proporcjonalne do masy ciała m. Kierunek i zwrot przyspieszenia pokrywa się z kierunkiem i zwrotem siły. Wzór wyrażający tę zależność ma postać

a→=F→m{displaystyle {vec {a}}={frac {vec {F}}{m}}}

W ruchu prostoliniowym |

W ruchu po linii prostej kierunek prędkości jest ustalony, więc można ją traktować tak jak wielkość skalarną. Wówczas przyspieszenie określa wzór:

a=dvdt{displaystyle a={frac {dv}{dt}}}

W ruchu jednostajnie zmiennym |

Gdy przyspieszenie jest stałe, wzór definicyjny przybiera postać

a=ΔvΔt{displaystyle a={frac {Delta v}{Delta t}}}

gdzie Δv jest przyrostem prędkości w czasie Δt.

Przyspieszenie w ruchu krzywoliniowym |

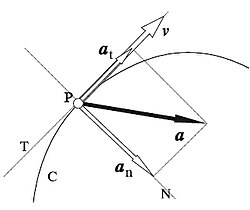
Przyspieszenie styczne a_t i normalne a_n

Jeżeli ciało porusza się po torze krzywoliniowym, wówczas całkowite przyspieszenie może być rozłożone na dwie składowe: prostopadłą do toru ruchu zwaną przyspieszeniem dośrodkowym lub normalnym (oznaczanym a→n{displaystyle {vec {a}}_{n}}) i składową równoległą zwaną przyspieszeniem stycznym (ozn. a→t{displaystyle {vec {a}}_{t}}).

Wektor przyspieszenia całkowitego jest sumą składowej normalnej i stycznej:

a→=a→n+a→t{displaystyle {vec {a}}={vec {a}}_{n}+{vec {a}}_{t}}

Składowe styczna i normalna są prostopadłe, dlatego wartość przyspieszenia całkowitego jest równa:

|a→|=|a→n|2+|a→t|2{displaystyle |{vec {a}}|={sqrt {|{vec {a}}_{n}|^{2}+|{vec {a}}_{t}|^{2}}}}

Przyspieszenie dośrodkowe (normalne) |

 Osobny artykuł: Przyspieszenie dośrodkowe.

Jest to składowa przyspieszenia prostopadła do toru ruchu. Reprezentuje tę część przyspieszenia, która wpływa na zmianę kierunku prędkości, a zatem na kształt toru, ale nie wpływa na zmianę wartości prędkości. Jeżeli prędkość chwilowa oznaczona jest jako v, a chwilowy promień zakrzywienia toru (promień okręgu stycznego do toru, czyli promień krzywizny toru) ruchu wynosi r, to wartość a_n przyspieszenia dośrodkowego ciała jest równa:

an=v2r{displaystyle a_{n}={frac {v^{2}}{r}}}

Przyspieszenie styczne |

Jest to składowa przyspieszenia styczna do toru ruchu, powodująca zmianę wartości prędkości, ale nie powodująca zmiany kierunku ruchu. Stosując oznaczenie v{displaystyle v} dla wartości prędkości chwilowej i oznaczenie s dla drogi pokonanej przez ciało, przyspieszenie styczne a_t określają wzory:

at=dvdt=d2sdt2{displaystyle a_{t}={frac {dv}{dt}}={frac {d^{2}s}{dt^{2}}}}

Przyspieszenie kątowe |

Przyspieszenie kątowe jest wielkością opisującą ruch krzywoliniowy utworzoną analogicznie do przyspieszenia, tylko wyrażoną w wielkościach kątowych. Jest pseudowektorem leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej. Jeśli współrzędną kątową ciała określa kąt α, a ω oznacza prędkość kątową, to wartość przyspieszenia kątowego ε określa wzór

ε=dωdt=d2αdt2[ε]=1s2{displaystyle varepsilon ={frac {domega }{dt}}={frac {d^{2}alpha }{dt^{2}}}quad left[varepsilon right]={frac {1}{{text{s}}^{2}}}}

Jednostką przyspieszenia kątowego w układzie SI jest jeden radian przez sekundę do kwadratu.

Przyspieszenie układu ciał |

Poniżej przedstawiono sposób obliczenia przyspieszenia przykładowego układu ciał.

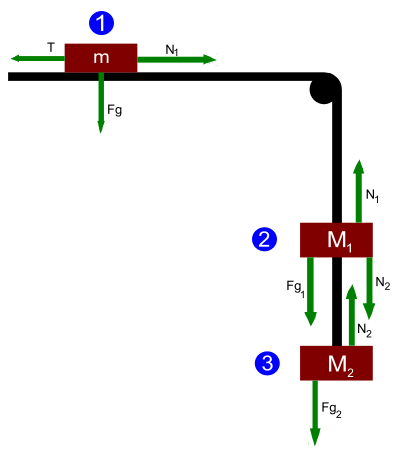
Aby wyznaczyć przyspieszenie poruszającego się układu ciał, należy sporządzić rysunek pomocniczy. Na rysunku rysujemy symbolicznie 3 ciała oraz działające na nie siły. Następnie należy ułożyć równanie siły wypadkowej dla każdego z ciał, bierzemy pod uwagę siły działające w kierunku ruchu ciała. Dla każdego ciała należy zapisać osobne równanie II zasady dynamiki.

Dla pierwszego ciała o masie m siła wypadkowa wynosi

Od naciągu odejmujemy tarcie, ponieważ ciało porusza się w prawą stronę i naciąg jest większy od tarcia.

Fw=N1−T{displaystyle F_{w}=N_{1}-T}

Zgodnie z II zasadą dynamiki siła wypadkowa równa się iloczynowi masy i przyspieszenia, a tarcie równa się iloczynowi masy, przyspieszenia ziemskiego i współczynnika tarcia. Zatem:

m⋅aw=N1−mgf{displaystyle mcdot a_{w}=N_{1}-mgf}

Kolejnym krokiem jest ułożenie równania siły wypadkowej dla ciała o masie M₁. Ciężar ciała i naciąg 2 są większe od naciągu 1, zatem równanie ma postać:

Fw=Fg1+N2−N1{displaystyle F_{w}=Fg_{1}+N_{2}-N_{1}}

Zgodnie z II zasadą dynamiki siła wypadkowa równa się iloczynowi masy i przyspieszenia, a ciężar ciała równa się iloczynowi masy i stałej grawitacji. Zatem:

M1⋅aw=M1⋅g+N2−N1{displaystyle M_{1}cdot a_{w}=M_{1}cdot g+N_{2}-N_{1}}

Przy okazji wyprowadzamy wzór na naciąg, który przyda się do dalszych obliczeń.

N1=M1⋅g+N2−M1⋅aw{displaystyle N_{1}=M_{1}cdot g+N_{2}-M_{1}cdot a_{w}}

W końcu układamy wzór na siłę wypadkową dla ciała o masie M₂

Fw=Fg2−N2{displaystyle F_{w}=Fg_{2}-N_{2}}

Zgodnie z II zasadą dynamiki siła wypadkowa równa się iloczynowi masy i przyspieszenia, a ciężar ciała równa się iloczynowi masy i stałej grawitacji. Zatem:

M2⋅aw=M2⋅g−N2{displaystyle M_{2}cdot a_{w}=M_{2}cdot g-N_{2}}

Wyprowadzamy wzór na naciąg 2.

N2=M2⋅g−M2⋅aw{displaystyle N_{2}=M_{2}cdot g-M_{2}cdot a_{w}}

Następnie do wzoru na naciąg 1 podstawiamy w miejsce N₂ wzór na naciąg 2

N1=M1⋅g+M2⋅g−M2⋅aw−M1⋅aw{displaystyle N_{1}=M_{1}cdot g+M_{2}cdot g-M_{2}cdot a_{w}-M_{1}cdot a_{w}}

Teraz za naciąg 1 podstawiamy m⋅aw=N1−mgf{displaystyle mcdot a_{w}=N_{1}-mgf}, przenosimy −mgf{displaystyle -mgf} na drugą stronę równania

m⋅aw=M1⋅g+M2⋅g−M2⋅aw−M1⋅aw−mgf{displaystyle mcdot a_{w}=M_{1}cdot g+M_{2}cdot g-M_{2}cdot a_{w}-M_{1}cdot a_{w}-mgf}

Kolejnym krokiem jest uporządkowanie równań, wyrażenia z przyspieszeniem przenosimy na lewo, a wyrazy z przyspieszeniem ziemskim na prawo

m⋅aw+M1⋅aw+M2⋅aw=M1⋅g+M2⋅g−mgf{displaystyle mcdot a_{w}+M_{1}cdot a_{w}+M_{2}cdot a_{w}=M_{1}cdot g+M_{2}cdot g-mgf}

Po lewej stronie równania wyciągamy przed nawias przyspieszenie wypadkowe, po prawej stronie podobnie postępujemy z przyspieszeniem ziemskim

aw(m+M1+M2)=g(M1+M2−mf){displaystyle a_{w}(m+M_{1}+M_{2})=g(M_{1}+M_{2}-mf)}

Następnie dzielimy równanie obustronnie przez (m+M1+M2){displaystyle (m+M_{1}+M_{2})} i otrzymujemy wyprowadzony wzór na przyspieszenie wypadkowe układu ciał.

aw=g(M1+M2−mf)m+M1+M2{displaystyle a_{w}={frac {g(M_{1}+M_{2}-mf)}{m+M_{1}+M_{2}}}}

Pomiar |

Do pomiaru służy przetwornik przyspieszenia nazywany przyspieszeniomierzem lub akceleromierzem czy akcelerometrem.

Zobacz też |

• 
  zryw – zmiana przyspieszenia w czasie


• przyspieszenie dośrodkowe


• przyspieszenie ziemskie


• przyspieszenie grawitacyjne


• grawitacja

p • d • e Mechanika klasyczna Działy Dynamika • Kinematyka • Mechanika nieba • Mechanika ośrodków ciągłych • Mechanika statystyczna • Mechanika stosowana • Statyka Sformułowania Formalizm Hamiltona • Formalizm Lagrange’a • Mechanika newtonowska Koncepcje podstawowe Bezwładność • Czas • Energia • Energia kinetyczna • Energia potencjalna • Grawitacja • Masa • Moc • Moment bezwładności • Moment pędu • Moment siły / Moment / Para sił • Popęd • Praca • Praca wirtualna • Przestrzeń • Przyspieszenie • Prędkość • Pęd • Siła • Szybkość • Układ odniesienia • Zasada d’Alemberta Podstawowe zagadnienia Bryła sztywna • Droga kątowa • Dynamika bryły sztywnej • Siła Coriolisa • Kinematyczne równanie ruchu • Oscylator harmoniczny • Nieinercjalny układ odniesienia • Obracający się układ odniesienia • Oś obrotu • Prawo powszechnego ciążenia • Przemieszczenie • Przyspieszenie kątowe • Prędkość kątowa • Prędkość obrotowa • Prędkość względna • Pulsacja • Ruch • Ruch harmoniczny • Ruch jednostajny prostoliniowy • Ruch obrotowy jednostajny • Ruch obrotowy niejednostajny • Ruch obrotowy • Równania Eulera (dynamika bryły sztywnej) • Siła bezwładności • Siła dośrodkowa • Siła odśrodkowa reakcji • Siła odśrodkowa • Tarcie • Tłumienie • Inercjalny układ odniesienia • Wahadło • Wibracje • Zasady dynamiki Newtona Znani uczeni Jean le Rond d’Alembert • Alexis Clairaut • Leonhard Euler • William Rowan Hamilton • Jeremiah Horrocks • Joseph Louis Lagrange • Pierre Simon de Laplace • Pierre Louis Maupertuis • Isaac Newton • Henri Poincaré • Siméon Denis Poisson