平方根

Multi tool use
Multi tool use




平方根（へいほうこん、英語: square root）とは、数に対して、平方すると元の値に等しくなる数のことである。与えられた数を面積とする正方形を考えるとき、その数の平方根の絶対値がその一辺の長さであり、一つの幾何学的意味付けができる。また、単位長さと任意の長さ x が与えられたとき、長さ x の平方根を定規とコンパスを用いて作図することができる。二乗根（にじょうこん）、自乗根（じじょうこん）とも言う。




目次






  • 1 定義


  • 2 いくつかの基本的なこと


  • 3 平方根函数


  • 4 負の数の平方根


  • 5 二次体


  • 6 複素数の平方根


  • 7 数以外の平方根


    • 7.1 行列の平方根


    • 7.2 可換整域および可換体の場合


    • 7.3 非可換または零因子を持つ環の場合




  • 8 脚注


  • 9 参考文献


  • 10 関連項目


  • 11 外部リンク





定義


数 a に対して、a = b2 を満たす b を a の平方根という。a がどのような数の範囲であるかによって、この概念は、意味を持つかどうかということを含め、さまざまな点で差異が生じるということに注意が必要である。


0 の平方根は 0 のみである。また、どんな正の数 a に対しても平方根は正と負の2つ存在し、そのうち正である方を根号（こんごう、radical symbol）{displaystyle {sqrt {;}}}{displaystyle {sqrt {;}}} を用いて


a{displaystyle {sqrt {a}}}{sqrt {a}}

と表し「正の（あるいは非負の）平方根」（principal square root; 主平方根）と呼ぶ（文脈上紛れのおそれの無いと思われるときは「正の」を省略することもある）。このとき、もう一方の「負の平方根」は −a{displaystyle -{sqrt {a}}}{displaystyle -{sqrt {a}}} と表すことができる。また、2つの平方根を併せて ±a{displaystyle pm {sqrt {a}}}{displaystyle pm {sqrt {a}}} と表記することもできる。例えば、16 の平方根は ±4、すなわち +4 と −4 の2つであり、16{displaystyle {sqrt {16}}}{displaystyle {sqrt {16}}}は正である 4 の方を表す。0{displaystyle {sqrt {0}}}{displaystyle {sqrt {0}}} は、0 の唯一の平方根 0 を意味すると約束する。根号に関するこれらの規約は、非負の実数の範囲でのみ通用する便宜的なものであることに注意を要する。


負の数の平方根は、考える数の範囲を複素数まで拡大すれば定義できる。また、数とは限らず、もっと一般にいくつかの数学的対象についても、それぞれに意味のある仕方で平方根が定義されるものがある（正定値行列など）。



いくつかの基本的なこと


a が正の整数でも、a の平方根は整数とは限らない。例えば 10{displaystyle {sqrt {10}}}{sqrt {10}} は小数表示すると 3.162277660168… と小数部分が循環せず、無理数である。平方根が整数であるような整数は平方数に限られる。そうでない整数の平方根は無理数となる（無限降下法または素因数分解の可能性・一意性から証明される）。正の整数や小数の平方根の小数表示を求めるには、開平法という筆算による方法が知られている。


a = x2y (x, y > 0) と表せるならば、その正の平方根について:a{displaystyle {sqrt {a}}}{sqrt {a}}= xy{displaystyle x{sqrt {y}}}x{sqrt {y}}が成り立つから、正の整数 a が平方因子を持つ場合は、根号内がより小さい表示にできる。 例えば 18 = 32 × 2 であるから、18=32{displaystyle {sqrt {18}}=3{sqrt {2}}}{displaystyle {sqrt {18}}=3{sqrt {2}}} と表せる。


比較的小さな数の平方根については、概数を知る必要がしばしばあることから、以下のような小数部分の数桁目までの語呂合わせが知られている。




  • 2=1.41421356⋯{displaystyle {sqrt {2}}=1.41421356cdots }{displaystyle {sqrt {2}}=1.41421356cdots } 一夜一夜に人見頃（ひとよひとよにひとみごろ）


  • 3=1.7320508075⋯{displaystyle {sqrt {3}}=1.7320508075cdots }{displaystyle {sqrt {3}}=1.7320508075cdots } 人並みに奢れや女子（ひとなみにおごれやおなご）


  • 5=2.2360679⋯{displaystyle {sqrt {5}}=2.2360679cdots }{displaystyle {sqrt {5}}=2.2360679cdots } 富士山麓鸚鵡鳴く（ふじさんろくおーむなく）

    • 「富士山麓に 鸚鵡鳴く」と誤って覚えるむきも多い。


    • 5=2.236067977⋯{displaystyle {sqrt {5}}=2.236067977cdots }{displaystyle {sqrt {5}}=2.236067977cdots } なので、小数点以下 8 桁ならば、切り捨てた「 2.2360679 」よりは、四捨五入した「 2.2360680 」の方が近い。




  • 6=2.4494897⋯{displaystyle {sqrt {6}}=2.4494897cdots }{displaystyle {sqrt {6}}=2.4494897cdots } ツヨシ串焼くな（つよしくしやくな）、煮よ良く弱く（によよくよわく）
    000≈ 2.44949 似よ良く良く（によよくよく）、二夜しくしく（によしくしく）


  • 7=2.64575⋯{displaystyle {sqrt {7}}=2.64575cdots }{displaystyle {sqrt {7}}=2.64575cdots } 菜 (7) に虫来ない（（な）にむしこない）、「菜に虫いない」とも。


  • 8=22=2.828427⋯{displaystyle {sqrt {8}}=2{sqrt {2}}=2.828427cdots }{displaystyle {sqrt {8}}=2{sqrt {2}}=2.828427cdots } ニヤニヤ呼ぶな（にやにやよぶな）


  • 10=3.162277⋯{displaystyle {sqrt {10}}=3.162277cdots }{displaystyle {sqrt {10}}=3.162277cdots } 父 (10) さん一郎兄さん（とうさんいちろーにーさん）


実数 x に対して、x2 ≥ 0 であり、


x2=|x|(={x(x≥0)−x(x≤0)){displaystyle {sqrt {x^{2}}}=|x|left(={begin{cases}x&(xgeq 0)\-x&(xleq 0)end{cases}}right)}{sqrt {x^{2}}}=|x|left(={begin{cases}x&(xgeq 0)\-x&(xleq 0)end{cases}}right)

が成り立つ。ここで |x| は x の絶対値である。また、x と y が非負のときには


xy=xyxy=xy{displaystyle {begin{aligned}{sqrt {xy}}&={sqrt {x}}{sqrt {y}}\{sqrt {frac {x}{y}}}&={frac {sqrt {x}}{sqrt {y}}}end{aligned}}}{begin{aligned}{sqrt {xy}}&={sqrt {x}}{sqrt {y}}\{sqrt {{frac {x}{y}}}}&={frac {{sqrt {x}}}{{sqrt {y}}}}end{aligned}}

が成り立つ。これらは（証明を述べれば明らかであるが）非負の実数に対してその非負の平方根が一意に定まるということに依存して成立しており、後述するように、根号内が負の数や虚数のときは、一般には成り立たない。


また、非負実数 x に対しては、その冪乗と冪根について


x=(x)2=(x24)2=(x36)2=⋯{displaystyle x=left({sqrt {x}}right)^{2}=left({sqrt[{4}]{x^{2}}}right)^{2}=left({sqrt[{6}]{x^{3}}}right)^{2}=cdots }{displaystyle x=left({sqrt {x}}right)^{2}=left({sqrt[{4}]{x^{2}}}right)^{2}=left({sqrt[{6}]{x^{3}}}right)^{2}=cdots }

が成り立ち、特に


x1/2:=x{displaystyle x^{1/2}:={sqrt {x}}}x^{{1/2}}:={sqrt {x}}

と定めることは（指数の表示 1/2 = 2/4 = 3/6 = … に依らずに一定という意味で）well-defined で、指数法則とも整合する。



平方根函数


入力 x に対してその非負の平方根 x{displaystyle {sqrt {x}}}{sqrt {x}} を返す函数 f(x)=x{displaystyle f(x)={sqrt {x}}}f(x)={sqrt {x}} を非負実数全体の集合 R+ ∪ {0} 上で定義されていると考えた正の平方根函数


∙:R+∪{0}∋x →1-1,onto x∈R+∪{0}{displaystyle {sqrt {bullet }}colon mathbb {R} ^{+}cup {0}ni x {xrightarrow {text{1-1,onto}}} {sqrt {x}}in mathbb {R} ^{+}cup {0}}{displaystyle {sqrt {bullet }}colon mathbb {R} ^{+}cup {0}ni x {xrightarrow {text{1-1,onto}}} {sqrt {x}}in mathbb {R} ^{+}cup {0}}

は（函数として well-defined で）、それ自身への全単射になる。正の平方根函数のグラフと負の平方根函数


−∙:R+∪{0}∋x →1-1,onto −x∈R−∪{0}{displaystyle {-{sqrt {bullet }}}colon mathbb {R} ^{+}cup {0}ni x {xrightarrow {text{1-1,onto}}} {-{sqrt {x}}}in mathbb {R} ^{-}cup {0}}{displaystyle {-{sqrt {bullet }}}colon mathbb {R} ^{+}cup {0}ni x {xrightarrow {text{1-1,onto}}} {-{sqrt {x}}}in mathbb {R} ^{-}cup {0}}

のグラフの和集合は、二次函数 y = x2 のグラフと直線 y = x に関して線対称な放物線に等しい。




正の平方根函数のグラフ。これは放物線の半分になっている。


正の平方根函数 √ は連続かつ x > 0 で微分可能であり、導関数は


ddxx=12x{displaystyle {frac {d}{dx}}{sqrt {x}}={frac {1}{2{sqrt {x}}}}}{frac {d}{dx}}{sqrt {x}}={frac {1}{2{sqrt {x}}}}

原始関数の一つは


∫xdx=23(x)3=23x32{displaystyle int {sqrt {x}},dx={frac {2}{3}}({sqrt {x}})^{3}={frac {2}{3}}x^{frac {3}{2}}}{displaystyle int {sqrt {x}},dx={frac {2}{3}}({sqrt {x}})^{3}={frac {2}{3}}x^{frac {3}{2}}}

で与えられる。また、収束冪級数としての二項展開


1+x=∑n=0∞(1/2n)xn=1+x2−x28+⋯=∑n=0∞(−1)n(2n)!(1−2n)(n!)2(4n)xn{displaystyle {sqrt {1+x}}=sum _{n=0}^{infty }{binom {1/2}{n}}x^{n}=1+{frac {x}{2}}-{frac {x^{2}}{8}}+cdots =sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}}{displaystyle {sqrt {1+x}}=sum _{n=0}^{infty }{binom {1/2}{n}}x^{n}=1+{frac {x}{2}}-{frac {x^{2}}{8}}+cdots =sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}}

が |x| < 1 で成り立つ。


x > 0 に対して自然数 n に関して帰納的に


fn(x)=x+x+x+x+...{displaystyle f_{n}(x)={sqrt {x+{sqrt {x+{sqrt {x+{sqrt {x+...}}}}}}}}}f_{n}(x)={sqrt {x+{sqrt {x+{sqrt {x+{sqrt {x+...}}}}}}}}

（x および根号の個数は n）と定めると、函数列 fn は漸化式


fn+1(x)2=x+fn(x){displaystyle f_{n+1}(x)^{2}=x+f_{n}(x)}f_{{n+1}}(x)^{2}=x+f_{n}(x)

に従い、fn(x) > 0 が α(x) > 0 に収束するならば α(x)2 − α(x) − x = 0 でなければならないから、


limn→∞fn(x)=x+14+12{displaystyle lim _{nto infty }f_{n}(x)={sqrt {x+{frac {1}{4}}}}+{frac {1}{2}}}lim _{{nto infty }}f_{n}(x)={sqrt {x+{frac {1}{4}}}}+{frac {1}{2}}

が成り立つ。



負の数の平方根


a < 0 の場合は、a の平方根は実数でなく、はっきりと指定することができない。複素数の範囲では、a の平方根の1つを b とすると、x2 = a の解は (x + b)(x − b) = 0 より x = ±b で、a の平方根は2つあると分かる。そこで、記号 a{displaystyle {sqrt {a}}}{sqrt {a}} は +b, −b のどちらを指すかが問題となる。


−1 の平方根の1つ（どちらでもよい）をあらかじめ指定しておき、それを i で表す（虚数単位と呼ぶ）。これにより、a の平方根は ±−ai{displaystyle pm {sqrt {-a}},i}{displaystyle pm {sqrt {-a}},i} と表せるから、


a=−ai{displaystyle {sqrt {a}}={sqrt {-a}},i}{sqrt {a}}={sqrt {-a}},i

と定めることにする。例えば −5=5i{displaystyle {sqrt {-5}}={sqrt {5}},i}{displaystyle {sqrt {-5}}={sqrt {5}},i} である。


正の数の平方根においてよく知られる計算法則


ab=ab{displaystyle {sqrt {a}}{sqrt {b}}={sqrt {ab}}}{sqrt {a}}{sqrt {b}}={sqrt {ab}}

は、a < 0 かつ b < 0 のとき成立しない。実際、左辺は


ab=−ai×−bi=−a−bi2=−ab{displaystyle {sqrt {a}}{sqrt {b}}={sqrt {-a}},itimes {sqrt {-b}},i={sqrt {-a}}{sqrt {-b}},i^{2}=-{sqrt {ab}}}{sqrt {a}}{sqrt {b}}={sqrt {-a}},itimes {sqrt {-b}},i={sqrt {-a}}{sqrt {-b}},i^{2}=-{sqrt {ab}}

なので、この場合


ab=−ab{displaystyle {sqrt {a}}{sqrt {b}}=-{sqrt {ab}}}{sqrt {a}}{sqrt {b}}=-{sqrt {ab}}

が正しい。


四元数や八元数においては、複数の虚数単位を定義し、a の平方根は2個より多くなる。



二次体


有理数体 Q（有理数全体（負の数も含む））上で定義される函数


Q∋x↦x∈A{displaystyle mathbb {Q} ni xmapsto {sqrt {x}}in mathbb {A} }{mathbb {Q}}ni xmapsto {sqrt {x}}in {mathbb {A}}

において、その値域は（虚数も含めた）代数的数（の一部）からなる。有理数の平方根が再び有理数となるならば、その有理数は（有理数の範囲での）平方数であるという。有理数内で平方数とならない有理数 d に対して √d は二次の無理数であって、Q に √d を付け加えて得られる体（たい）は二次体と総称される。



複素数の平方根


a が 0 でない複素数のとき、 b2 = a を満たす複素数 b は2個存在する。a の極形式を


a=reiθ (r>0,−π<θ≤π){displaystyle a=re^{itheta } (r>0,,-pi <theta leq pi )}a=re^{{itheta }} (r>0,,-pi <theta leq pi )

とすると、b の動径の2乗が r、b の偏角の2倍が θ であるから、


a=reiθ/2{displaystyle {sqrt {a}}={sqrt {r}},e^{itheta /2}}{sqrt {a}}={sqrt {r}},e^{{itheta /2}}

と定義すると、これは a に対して一意に定まり、(√a)2 = a を満たす。これを a の平方根の主値（しゅち、principal value）という。この主値により定義される平方根函数


C∋z↦z∈C{displaystyle mathbb {C} ni zmapsto {sqrt {z}}in mathbb {C} }{mathbb {C}}ni zmapsto {sqrt {z}}in {mathbb {C}}

は、実軸の負の部分を除くガウス平面 C の全域で至る所正則である。しかし実軸の負の部分上では連続でさえない。これを2枚のガウス平面を実軸の負の部分で張り合わせた平方根函数のリーマン面上で考えるならば、至る所解析的である。






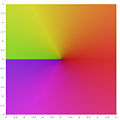
  • ガウス平面上の平方根函数を色で示したもの。原点の周りを偏角が正の方向（反時計回り）に回って、実軸の負の部分を跨ぐときもう一枚のガウス平面へ跳ぶ（緑→緑）。







  • もう一枚のガウス平面上の平方根函数。こちらもやはり原点を正の方向に回ると、実軸の負の部分を境に最初のガウス平面に帰る（紫→紫）。







  • 原点付近での平方根函数のリーマン面（2つのガウス平面を張り合わせたときの様子）
    平方根関数 Re z1/2
    ここで、z は複素数。






数以外の平方根



行列の平方根


詳細は「行列の平方根」を参照

一般に、正方行列 A に対して、A = B2 を満たす正方行列 B を A の平方根行列と呼び[1]、記号で √A あるいは A1⁄2 と表す。平方根行列は存在するとは限らず、存在しても1つだけの場合や複数個の場合、無限個存在する場合がある。例えば、二次単位行列 I2 は無数の平方根を持つ[2]。ただしその中で正定値となるのはただ一つ I2 自身である。


また、半正定値複素 (resp. 実) 正方行列 A に対して、A = BB*（あるいは A = B*B. ここに ∗ はエルミート共軛）を満たす（正方とは限らない）任意の行列 B をしばしば、 A の非エルミート (resp. 非対称) 平方根 (non-Hermitian (resp. symmetric) square root)[3] と呼ぶ（とくに適当な三角行列となるときコレスキー因子 (Cholesky factor)[4]とも呼ぶ）。B がそれ自身エルミート（実係数の場合は対称）ならば、これは上で述べた平方根の概念と一致する。任意の正定値エルミート行列 P に対し、それ自身正定値エルミートとなる平方根は一意であり、これを主平方根 (unique square root, principal square root)[5]と呼ぶが、しばしば記号 √P や P1/2 は専ら主平方根を表すために予約される[6]ことに注意すべきである。また、正定値エルミート行列の任意の非エルミート平方根は、ユニタリ行列を掛ける分の不定性を持つ[7]が、これは正実数の場合に、（正値の主平方根が一意に決まること、および）主平方根に ±1 を掛けたものがその平方根のすべてであることと対応している。


このような半正定値行列の平方根の計算および一意性の証明には、エルミート作用素に関するスペクトル論（固有値分解）や特異値分解あるいはコレスキー分解などが利用できる。[8][9][10]



可換整域および可換体の場合


（可換）整域の各元が二つより多くの平方根を持つことはない。実際、乗法の可換性により二平方数の差の公式（英語版） u2 − v2 = (u − v)(u + v) が成り立つことに注意すれば、u, v が同じ元の平方根であるとき u2 − v2 = 0, ゆえに零因子を持たないことから u = v または u + v = 0 であることが従う。後者は、二つの平方根が互いに加法逆元の関係にあることを言っているのだから、すなわち一つの元の平方根は（存在すれば）符号の違いを除いて一意である。特に、整域において零元 0 の平方根は 0 自身のみである。


標数 2 の可換体において、各元の平方根は一つ持つ（各元が自身を加法逆元にもつことに注意せよ）か、全く持たないかの何れかとなる（標数 2 の有限体においては任意の元が一意な平方根を持つ）。それ以外の任意の標数の体においては、先の段落のとおり任意の非零元が二つの平方根を持つか全く持たないかの何れかとなる。


奇素数 p と適当な正整数 e に対し q = pe と置く。q-元体 Fq の非零元が平方剰余であるとは、その平方根が Fq に属することを言い、さもなくば平方非剰余であるという。この体において (q − 1)/2 個の元が平方剰余であり、(q − 1)/2 個が非剰余である（零元はいずれのクラスにも属さないことに注意）。平方剰余元の全体は乗法に関して群を成す。この性質は代数的整数論において広く用いられる。



非可換または零因子を持つ環の場合


一般の環において、a の平方根 b を b2 = a のことと定めるならば、一般には平方根は符号を除いて一意とは限らない。


たとえば合同類環 Z/8Z を考えれば、この環において単位元 1 は相異なる四つの平方根を持つ（具体的には ±1, ±3）。他方、元 2 は平方根を持たない。詳細は平方剰余の項を参照されたい。


他の例として四元数体 H において、−1 は ±i, ±j, ±k を含む無数の平方根を持つ。実は −1 の平方根の全体はちょうど集合


{ai+bj+ck∣a2+b2+c2=1}{displaystyle {ai+bj+ckmid a^{2}+b^{2}+c^{2}=1}}{displaystyle {ai+bj+ckmid a^{2}+b^{2}+c^{2}=1}}

であり、したがって各平方根は絶対値が等しく、この集合は三次元空間内の二次元単位球面を描く。四元数#−1 の平方根も参照。


零元 0 の平方根は、定義により、0 自身または零因子である。四元数体のような可除環では零因子が存在しないから、一般に 0 の平方根は 0 のみである。しかし、零因子が存在しうる一般の環では必ずしもそうでないことは、反例として任意の自然数 n に対するZ/n2Z を考えればよい（この場合、n は零因子であり、実際に n2 = 0 を満たす）。



脚注





  1. ^ Higham, Nicholas J. (1986年4月). “Newton's Method for the Matrix Square Root”. en:Mathematics of Computation 46 (174): 537–549. doi:10.2307/2007992. http://www.ams.org/journals/mcom/1986-46-174/S0025-5718-1986-0829624-5/S0025-5718-1986-0829624-5.pdf. 


  2. ^ Mitchell, Douglas W., "Using Pythagorean triples to generate square roots of I2", Mathematical Gazette 87, November 2003, 499–500.


  3. ^ Marshall, Albert W.; Olkin, Ingram; Arnold, Barry, Inequalities, p. 773, https://books.google.com/books?id=I9wfajyOrooC&pg=PA773&dq=%22asymmetric%2Bsquare%2Broot%22 


  4. ^ Gentle, James E., Matrix Algebra, p. 194, https://books.google.com/books?id=PDjIV0iWa2cC&pg=PA194&dq=%22Cholesky+factor%22 


  5. ^ Higham, Nicholas J., Functions of Matrices, p. 20, https://books.google.com/books?id=2Wz_zVUEwPkC&pg=PA20&dq=%22unique%2Bsquare%2Broot%22 


  6. ^ Gentle, James E., Matrix Algebra, p. 125, https://books.google.com/books?id=PDjIV0iWa2cC&pg=PA125&dq=%22Cholesky+factor%22 


  7. ^ Lu, Andreas, Practical Optimization, p. 601, https://books.google.com/books?id=6_2RhaMFPLcC&pg=PA601&dq=%22non-hermitian%2Bsquare%2Broot%22 


  8. ^ Higham, Nicholas J., Functions of Matrices, p. 20, https://books.google.com/books?id=2Wz_zVUEwPkC&pg=PA20&dq=%22spectral%2Bdecomposition%22 


  9. ^ Gentle, James E., Matrix Algebra, p. 193, https://books.google.com/books?id=PDjIV0iWa2cC&pg=PA193&dq=%22nonnegative%2Bdefinite%22 


  10. ^ Lange, Kenneth, Numerical Analysis for Statisticians, p. 99, https://books.google.com/books?id=va4_AAAAQBAJ&pg=PA99&dq=%22unique%22 




参考文献



  • 一松信『2{displaystyle {sqrt {2}}}{sqrt {2}}の数学―無理数を見直す』海鳴社 ISBN 4875250568


関連項目



  • 平方数

  • 冪根

  • 多重根号

  • 二次体

  • リーマン面

  • ド・モアブルの定理



外部リンク




  • 数の泉 - ウェイバックマシン（2016年10月19日アーカイブ分）（2{displaystyle {sqrt {2}}}{sqrt {2}}や3{displaystyle {sqrt {3}}}{sqrt {3}}などを小数点以下100万桁まで掲載しているサイト）


  • 資料庫（平方根）（1{displaystyle {sqrt {1}}}{displaystyle {sqrt {1}}}から100{displaystyle {sqrt {100}}}{displaystyle {sqrt {100}}}までを小数点以下30桁まで掲載している）


  • Japanese soroban techniques - 加藤福太郎教授が考案した計算法（英語）

  • 2の平方根の求め方をまとめたサイト




uez,W,cVqmE2vPu YbVmrnVEZrb3tXKv8zM8i,3PAOxlMvfRyGwpQyjc6B fMPP 40gd
-
qtfJxwO1Fp8LiYT4V

Popular posts from this blog

冬

Image
季節による積雪の変化 冬 （ふゆ）は、四季の一つであり、一年の中で最も寒い期間・季節を指す。二十四節気や旧暦のように、一年中で最も太陽の高度が低く夜が長い期間を指すこともある。 北半球では冬至後の1月-2月頃に気温が低いことが多く、南半球では夏至後の7月‐8月頃にあたる。 日本の気象庁では一日の日最低気温が0℃以下の日を 冬日 （ふゆび）、また、日最高気温が0℃以下の日を 真冬日 （まふゆび）と呼んでいる。このような日は1月を中心に前後の毎年12月から翌年3月頃にかけて発生するから（ただし、年や地域によっては、11月・4月でも生じる場合もある）、この時期のあたりが冬の範囲に入る。 冬が特別・特有とされる物（特に収穫物）に付いては旬#冬を参照。 目次 1 定義 2 気候 3 生物 3.1 植物 3.2 動物 4 冬の行事 5 天文・自然 6 比喩的な用法 7 冬を題材にした作品 7.1 文学 7.2 音楽 7.2.1 クラシック 7.2.2 童謡 7.2.3 ポピュラー系 8 関連項目 定義 地球と太陽の光の模式図。この図では北半球が冬となる。 北半球が冬のときは南半球は太陽高度が高くなるため夏となり、南半球が冬のときは同様に北半球は夏となる。 社会通念・気象学では1月・2月・12月。たとえば「暖冬」「厳冬」などはこの3か月の平均気温で判断する。 寒候年・1年間の間で1月、2月、12月とすると1シーズンとしての冬を評価できない。そのため1月、2月を含む年をそのシーズンで括る。たとえば、「2009年の冬」といった場合、2008年の12月、2009年の1月、2月である。また、「2008/2009年冬」という書き方をする。初雪・終雪の日など11月以前、3月以降になることのあるようなものもこの定義による。 二十四節気に基づく節切りでは立冬から立春の前日まで。 旧暦による月切りでは十月・十一月・十二月。上に近いが、最大半月ずれる。 年度では1月・2月・3月。英語ではこの3か月をwinter quarterと呼ぶ。 天文学上は冬至から春分まで。ここでの「冬至」「春...
Read more

Fatturato

Image
Questa voce o sezione sull'argomento finanza aziendale non cita le fonti necessarie o quelle presenti sono insufficienti . Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Questa voce sull'argomento finanza aziendale è solo un abbozzo . Contribuisci a migliorarla secondo le convenzioni di Wikipedia. In economia aziendale il fatturato (detto anche volume d'affari ), secondo la corretta tecnica ragioneristico-tributaria, è la somma dei ricavi delle vendite [1] e/o delle prestazioni di servizi nonché degli altri ricavi e proventi ordinari di un'azienda registrati ai fini IVA per cui, quindi, è stata emessa fattura. I concetti, infatti, si ritrovano essenzialmente in ambito IVA. In un'accezione non tecnica e meramente corrente nel commercio, viene considerato volgarmente come la somma dei ricavi dell'impresa [2] . In realtà, il concetto di fatturato deriva diretta...
Read more

浄心駅

Image
浄心駅 浄心駅5番出口（2010年3月） じょうしん Joshin ◄ T03 庄内通 (1.4km) (0.8km) 浅間町 T05 ► 所在地 名古屋市西区城西四丁目3208 愛知県の地図を表示 名古屋市の地図を表示 北緯35度11分32秒 東経136度53分27秒 駅番号 ○ T04 所属事業者 名古屋市交通局 （名古屋市営地下鉄） 所属路線 鶴舞線 [1] キロ程 4.1km（上小田井起点） 駅構造 地下駅 ホーム 2面2線 乗車人員 -統計年度- 7,116人/日（降車客含まず） -2017年- 開業年月日 1981年（昭和56年）11月27日 [1] テンプレートを表示 浄心駅 （じょうしんえき）は、愛知県名古屋市西区城西4丁目にある、名古屋市営地下鉄鶴舞線の駅である。駅番号は T04 。 運行上の拠点であり乗務員の交代が当駅で行われる他、上り最終電車のみ当駅止まりとなる（翌朝当駅から上小田井駅へ回送し、上小田井駅発の列車となる）。かつては日中にも当駅起終点の列車が1往復設定されていた。 目次 1 歴史 2 駅構造 2.1 のりば 3 駅周辺 4 バス路線 5 隣の駅 6 脚注 7 関連項目 8 外部リンク 歴史 1981年（昭和56年）11月27日 - 当駅 - 伏見間の延伸に際し開業 [1] 。 1984年（昭和59年）9月6日 - 庄内緑地公園 - 当駅間の開業に伴い途中駅となる [1] 。 駅構造 浄心駅ホーム 相対式ホーム2面2線を有する地下駅。1番ホームには東改札口、2番ホームには西改札口がそれぞれあり、両ホームは線路の下を通る連絡通路でつながっている。改札外では東西それぞれのコンコースをつなぐ通路は無く、分断されている。 1番又は2番出入り口から入り階段を降りると1番ホーム（赤池・豊田市方面）にしか行けず、4～6番出入り口から入り階段を降りると2番ホーム（上小田井・犬山方面）にしか行くことができない。 よって、例えば2番ホームで降りて...
Read more