Jfyhkgu

Cet article ne cite pas suffisamment ses sources (novembre 2010).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références »

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En physique, un pseudovecteur ou vecteur axial est un vecteur de dimension 3 dont le sens dépend de l'orientation du trièdre de référence^[1]. C'est un objet mathématique qui se comporte de la même manière qu'un vecteur pour une rotation directe (conservant les angles orientés) mais différemment lors d'une isométrie indirecte, comme une symétrie par rapport à un point ou par rapport à un plan^[2].

La symétrie par rapport à l'origine d'une base orthonormale se traduit par un changement de signe des coordonnées du pseudovecteur. On parle de pseudovecteurs par opposition aux vecteurs dits vrais ou polaires, qui sont invariants par une telle inversion.

Les règles de calcul concernant les pseudovecteurs sont ainsi différentes de celles des vecteurs vrais. La raison en est qu'un pseudovecteur, même s'il possède comme un vecteur trois composantes liées au système de coordonnées choisi, n'est pas réellement un vecteur, mais un objet mathématique appelé forme différentielle de degré 2 (ou 2-forme), que l'on peut représenter par une matrice antisymétrique de trois lignes et trois colonnes, possédant donc seulement trois composantes indépendantes.

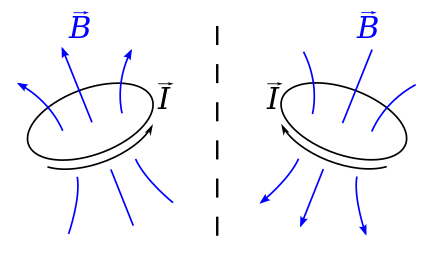
Une boucle de courant électrique (noir), crée un flux magnétique (bleu). Si on considère le système en miroir dans lequel le vecteur courant I est réfléchi, alors le pseudovecteur densité de flux magnétique B doit être réfléchi et inversé.

Définition |

Un pseudovecteur est un objet mathématique possédant, comme un vrai vecteur, une direction, un sens et un module (plus éventuellement une position), mais qui se comporte différemment lors d'une symétrie (par rapport à un point ou par rapport à un plan) ou lors d'un changement de référentiel (d'un trièdre direct à un trièdre inverse, ou réciproquement), cf. ci-dessous.

Notation |

On peut distinguer les pseudovecteurs des vecteurs axiaux en les notant avec une flèche courbée (dans le sens antihoraire), rappelant le caractère pseudovectoriel d'une rotation. Exemple : ω↪{displaystyle {overset {hookrightarrow }{omega }}} pour le pseudovecteur vitesse de rotation.

Généralités |

Sous une inversion les deux vecteurs changent de signe, mais le produit vectoriel est invariant [les deux vecteurs originaux sont en noir, les vecteurs inversés sont en gris et leur produit vectoriel commun est en rouge].

Les pseudovecteurs sont souvent construits à partir d'un produit vectoriel (de deux vecteurs polaires) ou d'un rotationnel (d'un vecteur polaire).

Si a→{displaystyle {vec {a}}} et b→{displaystyle {vec {b}}} sont deux vecteurs vrais (polaires), l'objet p↪{displaystyle {overset {hookrightarrow }{p}}} défini par

p↪=a→∧b→{displaystyle {overset {hookrightarrow }{p}}={vec {a}}wedge {vec {b}}}

est un pseudovecteur. Si l'on transforme tous les axes en leurs opposés, les vecteurs polaires sont transformés en leurs opposés (a→{displaystyle {vec {a}}} est remplacé par −a→{displaystyle -{vec {a}}}, et b→{displaystyle {vec {b}}} par −b→{displaystyle -{vec {b}}}). Si p↪{displaystyle {overset {hookrightarrow }{p}}} était un vecteur polaire, son image par cette transformation devrait être −p↪{displaystyle -{overset {hookrightarrow }{p}}} or, en utilisant la formule de calcul du produit vectoriel, on s'aperçoit que p↪{displaystyle {overset {hookrightarrow }{p}}} est invariant par une telle transformation : p↪{displaystyle {overset {hookrightarrow }{p}}} n'obéit pas aux mêmes règles de transformation que les « vrais » vecteurs, d'où ce nom de pseudovecteur.

Ce concept peut être généralisé : on parlera de pseudoscalaires et de pseudotenseurs pour des quantités qui ne respectent pas toutes les règles de calcul des scalaires et des tenseurs.

L'opérateur rotationnel, produit vectoriel avec l'opérateur nabla, construit également des pseudovecteurs.

La notion de pseudovecteur est particulièrement importante dans l'analyse des propriétés de symétrie des champs de vecteurs. Ainsi, si le champ électrique E→{displaystyle {vec {E}}} (vecteur vrai) possède les mêmes symétries que ses sources (un plan de symétrie des charges est plan de symétrie de E→{displaystyle {vec {E}}}), le champ magnétique B↪{displaystyle {overset {hookrightarrow }{B}}} inverse ces propriétés (un plan de symétrie des courants est plan d'antisymétrie de B↪{displaystyle {overset {hookrightarrow }{B}}}).

Un pseudovecteur est un tenseur d'ordre 2 antisymétrique et possède trois composantes dans un espace à trois dimensions.

Signification |

Les pseudovecteurs peuvent être utilisés pour représenter :

• des angles dans un plan de l'espace (pseudovecteurs 1-fois covariants 1-fois contravariants : c'est-à-dire ceux dont la norme est un scalaire vrai, comme les angles). Intuitivement, ces pseudovecteurs correspondent à une notion d'angle dans un plan de l'espace ;


• des éléments de surfaces orientées dans l'espace (pseudovecteurs 2-fois contravariants : leur norme est un scalaire doublement contravariant, comme les aires) ;


• une répartition surfacique en un point de l'espace. (pseudovecteurs 2-fois covariants, équivalents à des formes bilinéaires alternées).

L'idée qui relie les trois significations est celle de plan, de surface plane.

Exemples physiques |

Exemples de pseudovecteurs en physique :

• le moment cinétique, moment de la quantité de mouvement (LO↪=OM→∧p→{displaystyle {overset {hookrightarrow }{L_{mathrm {O} }}}={overrightarrow {mathrm {OM} }}wedge {vec {p}}}) ;


• le moment d'une force (ΓO↪=OM→∧F→{displaystyle {overset {hookrightarrow }{Gamma _{mathrm {O} }}}={overrightarrow {mathrm {OM} }}wedge {vec {F}}}) ;


• le champ magnétique (loi de Biot et Savart : dB↪=(μ0I4π)r→∧dl→r3{displaystyle {overset {hookrightarrow }{mathrm {d} B}}=left({frac {mu _{0}I}{4pi }}right){frac {{vec {r}}wedge {vec {mathrm {d} l}}}{r^{3}}}}) ;


• le moment magnétique (dμ↪=12r→∧j→dV{displaystyle {overset {hookrightarrow }{mathrm {d} mu }}={frac {1}{2}},{vec {r}}wedge {vec {j}};mathrm {d} V}) ;


• la vorticité d'un fluide, rotationnel du champ de vitesse (ω↪=rot↪(v→){displaystyle {overset {hookrightarrow }{omega }}={overset {hookrightarrow }{operatorname {rot} }}({vec {v}})}) ;


• la vitesse angulaire.

Le produit vectoriel du pseudovecteur vitesse angulaire et du vecteur rayon jusqu'au centre de rotation donne la vitesse du point considéré : c'est la formule de Varignon.

Le produit vectoriel du pseudovecteur accélération angulaire et du rayon vecteur donne l'accélération du point considéré.

Symétries |

Symétrie par rapport à un point |

Dans une symétrie S_O par rapport à un point O, un pseudovecteur reste invariant (alors qu'un vecteur polaire est transformé en son opposé).

Symétrie par rapport à un plan |

Dans une symétrie S_P par rapport à un plan P, la composante normale (au plan) d'un pseudovecteur reste invariante et sa composante parallèle est transformée en son opposée (alors que c'est le contraire pour un vecteur polaire).

Règles de calcul |

On portera attention au fait que si les calculs sont effectués en base orthonormée, il peut y avoir confusion entre vecteur/covecteur/pseudovecteur. Ces règles de calcul peuvent servir à lever les ambiguïtés et pouvoir alors changer de base.

Produit vectoriel |

• Si a→{displaystyle {vec {a}}} et b→{displaystyle {vec {b}}} sont des vecteurs vrais (des vecteurs polaires), l'objet défini par p↪=a→∧b→{displaystyle {overset {hookrightarrow }{p}}={vec {a}}wedge {vec {b}}} est un pseudovecteur.


• Si a→{displaystyle {vec {a}}} est un vecteur vrai et b↪{displaystyle {overset {hookrightarrow }{b}}} un pseudovecteur, l'objet défini comme précédemment est un vecteur vrai : p→=a→∧b↪{displaystyle {vec {p}}={vec {a}}wedge {overset {hookrightarrow }{b}}}.


• Il en est de même pour le produit vectoriel d'un pseudovecteur et d'un vecteur vrai : p→=a↪∧b→{displaystyle {vec {p}}={overset {hookrightarrow }{a}}wedge {vec {b}}} (c'est notamment le cas du vecteur de Poynting en électromagnétisme).


• Si a↪{displaystyle {overset {hookrightarrow }{a}}} et b↪{displaystyle {overset {hookrightarrow }{b}}} sont des pseudovecteurs, l'objet défini comme précédemment est un pseudovecteur : p↪=a↪∧b↪{displaystyle {overset {hookrightarrow }{p}}={overset {hookrightarrow }{a}}wedge {overset {hookrightarrow }{b}}}.

Addition |

• L'addition ou la soustraction de deux pseudovecteurs est un pseudovecteur.


• L'opposé d'un pseudovecteur est un pseudovecteur.


• On n'additionne pas un pseudovecteur avec un vecteur ou un covecteur.


• On n'additionne pas des pseudovecteurs de types différents.

Multiplication par un scalaire vrai |

• La multiplication d'un pseudovecteur par un scalaire vrai est un pseudovecteur de même type.


• La multiplication d'un vecteur vrai par un scalaire est un vecteur vrai.

Produit scalaire |

• Le produit scalaire d'un vecteur vrai et d'un covecteur est un scalaire vrai.


• Le produit scalaire de deux pseudovecteurs est un scalaire vrai.

Norme |

La norme d'un pseudovecteur est un scalaire. Elle se calcule par la formule a2+b2+c2{displaystyle {sqrt {a^{2}+b^{2}+c^{2}}}} où a, b et c sont les coordonnées du pseudovecteur dans la base orthonormale choisie.

Changement de base |

Les pseudovecteurs obéissent à des formules de changement de base différentes de celles des vecteurs vrais.

Les bases des pseudovecteurs sont différentes de celle des vecteurs vrais : en base orthonormée, cela se traduit par des changements de signe ; en base quelconque par des changements de toutes les coordonnées entre un vecteur et le pseudovecteur de même direction. Si on écrit pseudovecteurs et vecteurs vrais dans ce qui semble être une même base (i, j, k), il faudra de nouveau distinguer les bases lors d'opérations comme la symétrie plane.

Produit mixte |

Le produit mixte est défini par le déterminant :

Det(a,b,c)=a⋅(b∧c){displaystyle mathrm {Det} {bigl (}{boldsymbol {a}},{boldsymbol {b}},{boldsymbol {c}}{bigr )}={boldsymbol {a}}cdot ({boldsymbol {b}}wedge {boldsymbol {c}})}.

Si a est un pseudovecteur et b et c des vecteurs vrais, le résultat est un scalaire vrai. Dans les autres cas, il faut se référer à la définition du produit mixte.

Torseurs |

• La résultante d'un torseur est un vecteur vrai dans le cas d'un torseur cinétique, dynamique ou statique.


• La résultante d'un torseur est un pseudovecteur dans le cas d'un torseur cinématique.


• Le moment d'un torseur est un pseudovecteur dans le cas d'un torseur cinétique, dynamique ou statique.


• Le moment d'un torseur est un vecteur vrai dans le cas d'un torseur cinématique.

Rotationnel et divergence |

Rotationnel |

Le rotationnel d'un champ de vrais vecteurs est un pseudovecteur. Ce pseudovecteur est du type 1 fois covariant, 1 fois contravariant.

En revanche, pour un champ de pseudovecteurs, il existe une contradiction entre deux approches :

• si on garde les mêmes formules que pour les vecteurs (alors qu'on travaille dans une autre base!), le rotationnel est un vrai vecteur. C'est la définition la plus courante. L'exemple le plus connu est celui des équations de Maxwell : le rotationnel du pseudovecteur champ magnétique B est proportionnel au vecteur courant, qui est un vecteur vrai :
  

  
  ∇∧B=μ0(j+jD){displaystyle {boldsymbol {nabla }}wedge {boldsymbol {B}}=mu _{0}left({boldsymbol {j}}+{boldsymbol {j}}_{rm {D}}right)} ;

  
  


• en suivant la deuxième approche, les pseudovecteurs se comportant dans tous les cas comme des tenseurs du second ordre antisymétriques, on les analyse comme tels. Et alors on utilise la définition du rotationnel donnée pour les tenseurs du second ordre. Il apparaît alors quelque chose d'extraordinaire : le rotationnel d'un champ de pseudovecteurs calculé suivant cette définition a la même formule dans la base canonique des pseudovecteurs, que la divergence pour les champs de vecteurs vrais dans la base canonique des vecteurs vrais. C'est-à-dire que l'appellation usuelle de l'opérateur rotationnel pour les champs de pseudovecteurs est la divergence. Et cela est toujours nul ;

Divergence |

La divergence d'un champ de vrais vecteurs est un scalaire. En revanche, la divergence d'un champ de pseudovecteurs est toujours nulle. C'est la définition la plus courante, l'exemple usuel étant, à nouveau, le champ magnétique.

Synthèse |

• Ce que l'on appelle communément rotationnel, a effectivement pour les vecteurs vrais la signification de rotationnel : les pseudovecteurs représentent bien des rotations. Mais ceci a pour les pseudovecteurs la signication physique d'une divergence. Et pour les tenseurs du second ordre celle-ci est un vecteur.


• Ce que l'on appelle communément divergence est toujours nul pour les pseudovecteurs.

Représentation matricielle |

Un pseudovecteur peut être représenté par un tenseur antisymétrique d'ordre 2, avec 3 possibilités : soit le tenseur est 2 fois contravariant, soit 1 fois contravariant-1 fois covariant, soit 2 fois covariant. Seul le 2^e cas correspond à une matrice usuelle, où l'action d'un tel tenseur sur un vecteur donne à nouveau un vecteur.

Dans ce cas, en base orthonormale, la matrice :

(0−cbc0−a−ba0){displaystyle {begin{pmatrix}0&-c&b\c&0&-a\-b&a&0\end{pmatrix}}},

correspond au pseudovecteur usuellement représenté par :

(abc){displaystyle {begin{pmatrix}a\b\cend{pmatrix}}}.

Cette représentation par matrice carrée est particulièrement adaptée car :

• le produit vectoriel avec un vecteur vrai se traduit par une simple multiplication matricielle (attention cependant au signe, et à l'ordre des facteurs) ;


• le produit vectoriel avec un autre pseudovecteur se traduit par le crochet de Lie des deux matrices. [A, B] = AB - BA ; il est nul si et seulement si les deux matrices commutent ;


• les changements de base sont identiques aux changements de base des tenseurs d'ordre 2, voire à ceux des matrices quand il s'agit d'un tenseur 1 fois contravariant-1 fois covariant ;


• elle permet de voir facilement qu'un pseudovecteur correspond à une matrice de rotation d'un quart de tour dans un plan suivie ou précédée d'une projection sur ce plan ;


• en dimension 2, le produit vectoriel des deux vecteurs de base du plan correspond à une matrice antisymétrique :

(0−110){displaystyle {begin{pmatrix}0&-1\1&0\end{pmatrix}}}

Avec cette matrice, on peut représenter les nombres complexes. Le produit matriciel de cette matrice avec elle-même donne en effet l'opposé de la matrice identité. Et elle permet aussi par combinaison linéaire, de représenter les similitudes planes directes.

Exponentielle |

L'exponentielle de la matrice qui représente des pseudovecteurs en dimension 3 est une matrice de rotation, d'angle (en radians) a2+b2+c2{displaystyle {sqrt {a^{2}+b^{2}+c^{2}}}}, dont la direction est donnée par le pseudovecteur.

Généralisation : tenseurs |

Les notions de variance/covariance sont issues du formalisme des tenseurs.

Ce formalisme permet d'étendre les notions de vecteur, covecteur et pseudovecteur à des espaces de dimension plus grande que 3.

Notes et références |

Voir aussi |

Articles connexes |

• Matrice antisymétrique


• 
  Pseudoscalaire, Scalaire
  


• 
  Covecteur , Espace dual
  


• Tenseur


• Analyse vectorielle


• Orientation


• Grandeur d'orientation

Liens externes |

• 
  www.isima.fr/~leborgne/IsimathMeca/Produitvectoriel.pdf. "Produit vectoriel, pseudo-produit vectoriel, et endomorphismes antisymétriques". 9 pages.

v · m Algèbre linéaire générale
Vecteur Scalaire Combinaison linéaire Espace vectoriel Matrice
Famille de vecteurs	Famille génératrice Famille libre (indépendance linéaire) Base Théorème de la base incomplète Rang Colinéarité
Sous-espace	Sous-espace vectoriel Somme de Minkowski Somme directe Sous-espace supplémentaire Dimension Codimension Droite Plan Hyperplan
Morphisme et notions relatives	Application linéaire Noyau Conoyau Lemme des noyaux Pseudo-inverse Théorème de factorisation Théorème du rang Équation linéaire Système d'équations linéaires Élimination de Gauss-Jordan Forme linéaire Espace dual Orthogonalité Base duale Endomorphisme linéaire Valeur propre, vecteur propre et espace propre Projecteur Symétrie Matrice diagonalisable Diagonalisation Endomorphisme nilpotent
Dimension finie	Espace vectoriel de dimension finie Trace Déterminant Polynôme caractéristique Polynôme d'endomorphisme Théorème de Cayley-Hamilton Polynôme minimal d'un endomorphisme Invariants de similitude Réduction d'endomorphisme Réduction de Jordan Décomposition de Dunford Décomposition de Frobenius
Enrichissements de structure	Norme Produit scalaire Forme quadratique Espace vectoriel topologique Orientation Algèbre sur un corps Algèbre de Lie Complexe différentiel
Développements	Théorie des matrices Représentation de groupe Analyse fonctionnelle Algèbre multilinéaire Module sur un anneau

• Portail de la physique
• Portail des mathématiques