Теория Друде







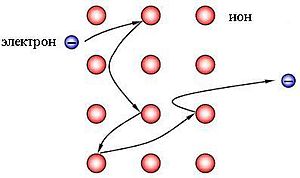
Электрическое поле ускоряет электроны находящиеся в электронном газе. Соударения с дефектами решётки замедляют их.


Теория Друде — классическое описание движения электронов в металлах. Эта теория была предложена немецким физиком Паулем Друде через 3 года после открытия электрона как частицы — в 1900 году. Она отличается простотой и наглядностью, хорошо поясняет эффект Холла, удельную проводимость в постоянном и переменном токе и теплопроводность в металлах и поэтому до сегодняшнего дня актуальна. Может использоваться для нескольких типов носителей включая пространственно разделённые слои как в кулоновском увлечении.




Содержание






  • 1 Основные предположения


  • 2 Формула Друде


  • 3 Некоторые формулы


  • 4 Пределы применимости


  • 5 Литература





Основные предположения |


Электроны в металле рассматриваются как электронный газ, к которому можно применить кинетическую теорию газов. Считается, что электроны, как и атомы газа в кинетической теории, представляют собой одинаковые твёрдые сферы, которые движутся по прямым линиям до тех пор, пока не столкнутся друг с другом. Предполагается, что продолжительность отдельного столкновения пренебрежимо мала, и что между молекулами не действует никаких иных сил, кроме возникающих в момент столкновения. Так как электрон — отрицательно заряженная частица, то для соблюдения условия электронейтральности в твёрдом теле также должны быть частицы другого сорта — положительно заряженные. Друде предположил, что компенсирующий положительный заряд принадлежит гораздо более тяжёлым частицам (ионам), которые он считал неподвижными. Во времена Друде не было ясно, почему в металле существуют свободные электроны и положительно заряженные ионы, и что эти ионы собой представляют. Ответы на эти вопросы смогла дать только квантовая теория твёрдого тела. Для многих веществ, однако, можно просто считать, что электронный газ составляют слабо связанные с ядром внешние валентные электроны, которые в металле «освобождаются» и получают возможность свободно передвигаться по металлу, тогда как атомные ядра с электронами внутренних оболочек (атомные остовы) остаются неизменными и играют роль неподвижных положительных ионов теории Друде.


Несмотря на то, что плотность газа электронов проводимости примерно в 1000 раз больше плотности классического газа при нормальных температуре и давлении, и несмотря на присутствие сильного электрон-электронного и электрон-ионного взаимодействия в модели Друде для рассмотрения электронного газа в металлах почти без изменений применяются методы кинетической теории нейтральных разреженных газов.


Основные предположения теории Друде.



  • В интервале между столкновениями не учитывается взаимодействие электрона с другими электронами и ионами. Иными словами, принимается, что в отсутствие внешних электромагнитных полей каждый электрон движется с постоянной скоростью по прямой линии. Далее, считают, что в присутствии внешних полей электрон движется в соответствии с законами Ньютона; при этом учитывают влияние только этих полей, пренебрегая сложными дополнительными полями, порождаемыми другими электронами и ионами. Приближение, в котором пренебрегают электрон-электронным взаимодействием в промежутках между столкновениями, известно под названием приближения независимых электронов. Соответственно приближение, в котором пренебрегают электрон-ионным взаимодействием, называется приближением свободных электронов.

  • В модели Друде, как и в кинетической теории, столкновения — это мгновенные события, внезапно меняющие скорость электрона. Друде связывал их с тем, что электроны отскакивают от непроницаемых сердцевин ионов (а не считал их электрон-электронными столкновениями по аналогии с доминирующим механизмом столкновений в обычном газе).

  • Предполагается, что за единицу времени электрон испытывает столкновение (то есть внезапное изменение скорости) с вероятностью, равной 1τ{displaystyle {1 over tau }}{1 over tau }. Имеется в виду, что для электрона вероятность испытать столкновение в течение бесконечно малого промежутка времени dt{displaystyle dt}dt равна просто dtτ{displaystyle {dt over tau }}{dt over tau }. Время τ{displaystyle tau }tau называют временем релаксации, или временем свободного пробега; оно играет фундаментальную роль в теории проводимости металлов. Из этого предположения следует, что электрон, выбранный наугад в настоящий момент времени, будет двигаться в среднем в течение времени τ{displaystyle tau }tau до его следующего столкновения и уже двигался в среднем в течение времени τ{displaystyle tau }tau с момента предыдущего столкновения. В простейших приложениях модели Друде считают, что время релаксации τ{displaystyle tau }tau не зависит от пространственного положения электрона и его скорости.

  • Предполагается, что электроны приходят в состояние теплового равновесия со своим окружением исключительно благодаря столкновениям. Считается, что столкновения поддерживают локальное термодинамическое равновесие чрезвычайно простым способом: скорость электрона сразу же после столкновения не связана с его скоростью до столкновения, а направлена случайным образом, причём её величина соответствует той температуре, которая превалирует в области, где происходило столкновение. Поэтому чем более горячей является область, где происходит столкновение, тем большей скоростью обладает электрон после столкновения.



Формула Друде |


Кинетическое уравнение Больцмана в приближении времени релаксации приводит для проводимости электронного газа к формуле Друде:


σ=ne02τ2m∗{displaystyle sigma ={frac {ne_{0}^{2}tau }{2m^{*}}}}{displaystyle sigma ={frac {ne_{0}^{2}tau }{2m^{*}}}}



  • σ{displaystyle sigma }sigma  — электрическая удельная проводимость


  • n{displaystyle n}n — концентрация электронов


  • e0{displaystyle e_{0}}e_{0} — элементарный заряд


  • τ{displaystyle tau }tau  — время релаксации по импульсам (время, за которое электрон «забывает» о том в какую сторону двигался)


  • m∗{displaystyle m^{*}}m^{{*}} — эффективная масса электрона


Ниже приведён вывод этого выражения для классического случая без учёта реального потенциала рассеяния. Эта формула применима также к электронному и дырочному газу в полупроводниках (Формулу можно записать в другом виде для вырожденного электронного или дырочного газа σ=e02Dg{displaystyle sigma =e_{0}^{2}Dg}sigma =e_{0}^{2}Dg, где D{displaystyle D}D — коэффициент диффузии электронов или дырок, а g{displaystyle g}g — плотность электронных или дырочных состояний, причём все физические величины берутся на поверхности Ферми).
Плотности состояний в двумерном проводнике



g=gsgvm∗2πℏ2{displaystyle g=g_{s}g_{v}{frac {m^{*}}{2pi hbar ^{2}}}}{displaystyle g=g_{s}g_{v}{frac {m^{*}}{2pi hbar ^{2}}}},

где gs — спиновое вырождение, gv — долинное вырождение, m* — эффективная масса и не зависит от энергии. gs = 2 а долинное вырождение для GaAs gv = 1.


Для носителей тока с параболическим законом дисперсии (энергия отсчитывается от дна зоны проводимости)



EF=mvF22{displaystyle E_{F}={frac {mv_{F}^{2}}{2}}}{displaystyle E_{F}={frac {mv_{F}^{2}}{2}}},

где νF — скорость носителей на уровне Ферми, и g = n/EF, можно получить выражение Друде для двумерно электронного газа



σ=e02DnEF=2e02nDm∗vF2=ne02m∗2DvF2=ne02m∗τ{displaystyle sigma =e_{0}^{2}D{frac {n}{E_{F}}}={frac {2e_{0}^{2}nD}{m^{*}v_{F}^{2}}}={frac {ne_{0}^{2}}{m^{*}}}{frac {2D}{v_{F}^{2}}}={frac {ne_{0}^{2}}{m^{*}}}tau }{displaystyle sigma =e_{0}^{2}D{frac {n}{E_{F}}}={frac {2e_{0}^{2}nD}{m^{*}v_{F}^{2}}}={frac {ne_{0}^{2}}{m^{*}}}{frac {2D}{v_{F}^{2}}}={frac {ne_{0}^{2}}{m^{*}}}tau },

где последнее уравнение следует из условия вырожденности электронного газа и определения коэффициента диффузии.



Некоторые формулы |


  • ускорение электрона между двумя соударениями из второго закона Ньютона:

dv→dt=−e0m⋅E→{displaystyle {frac {d{vec {v}}}{dt}}=-{frac {e_{0}}{m}}cdot {vec {E}}}{frac {d{vec {v}}}{dt}}=-{frac {e_{0}}{m}}cdot {vec E}


  • средняя скорость электрона:

v¯=vd=−e0⋅E2m⋅τ{displaystyle {overline {v}}=v_{d}=-{frac {e_{0}cdot E}{2m}}cdot {tau }}{displaystyle {overline {v}}=v_{d}=-{frac {e_{0}cdot E}{2m}}cdot {tau }}

Следует, однако, иметь в виду, что мгновенная скорость электрона в металле может быть большой и определяется уровнем Ферми.



  • плотность тока:

j→=−n⋅e0⋅v→d{displaystyle {vec {j}}=-ncdot e_{0}cdot {vec {v}}_{d}}{vec j}=-ncdot e_{0}cdot {vec v}_{d}


  • Закон Ома:

j→=n⋅e02⋅τ2m⋅E→=σ⋅E→{displaystyle {vec {j}}={frac {ncdot e_{0}^{2}cdot tau }{2m}}cdot {vec {E}}=sigma cdot {vec {E}}}{displaystyle {vec {j}}={frac {ncdot e_{0}^{2}cdot tau }{2m}}cdot {vec {E}}=sigma cdot {vec {E}}}


  • подвижность носителей заряда:

μ=|v→d||E→|=e0⋅τ2m{displaystyle mu ={frac {|{vec {v}}_{d}|}{|{vec {E}}|}}={frac {e_{0}cdot tau }{2m}}}{displaystyle mu ={frac {|{vec {v}}_{d}|}{|{vec {E}}|}}={frac {e_{0}cdot tau }{2m}}}


  • тепловая энергия электрона:

Wth=3kT2{displaystyle W_{th}=3{frac {kT}{2}}}W_{{th}}=3{frac {kT}{2}}


Пределы применимости |


К недостаткам этой теории следует отнести то что эта теория феноменолоническая и использует время релаксации, которое нужно получить из эксперимента или более глубокой теории. Также использование кинетического уравнения Больцмана в приближении времени релаксации ограничивает применимость этой терии в области дискретного спектра носителей тока, то есть она применима только в квазиклассическом приближении, а в сильных магнитных полях (при формировании уровней Ландау) или при малом количестве мод (квантование сопротивления) не может адекватно описать физические явления. Также при макроскопическом проявлении квантовых эффектов как например явление сверхпроводимости. Даже в слабых магнитных полях теория Друде может терять применимость благодаря явлениям возникающим только в квантовой механике связанными с интерференцией, например слабая локализация, эффект Ааронова — Бома, универсальные флуктуации кондактанса. Кроме того даже сильная локализация (сильный беспорядок), перколяционная теория (низкая концентрация носителей), прыжковая проводимость и баллистический транспорт оказываются за пределеми применимости этой теории.



Литература |


  • Н. Ашкрофт, Н. Мермин. Физика твердого тела: В двух томах / М.И Каганов. — М.: Мир, 1979.







-

Popular posts from this blog

冬

Image
季節による積雪の変化 冬 （ふゆ）は、四季の一つであり、一年の中で最も寒い期間・季節を指す。二十四節気や旧暦のように、一年中で最も太陽の高度が低く夜が長い期間を指すこともある。 北半球では冬至後の1月-2月頃に気温が低いことが多く、南半球では夏至後の7月‐8月頃にあたる。 日本の気象庁では一日の日最低気温が0℃以下の日を 冬日 （ふゆび）、また、日最高気温が0℃以下の日を 真冬日 （まふゆび）と呼んでいる。このような日は1月を中心に前後の毎年12月から翌年3月頃にかけて発生するから（ただし、年や地域によっては、11月・4月でも生じる場合もある）、この時期のあたりが冬の範囲に入る。 冬が特別・特有とされる物（特に収穫物）に付いては旬#冬を参照。 目次 1 定義 2 気候 3 生物 3.1 植物 3.2 動物 4 冬の行事 5 天文・自然 6 比喩的な用法 7 冬を題材にした作品 7.1 文学 7.2 音楽 7.2.1 クラシック 7.2.2 童謡 7.2.3 ポピュラー系 8 関連項目 定義 地球と太陽の光の模式図。この図では北半球が冬となる。 北半球が冬のときは南半球は太陽高度が高くなるため夏となり、南半球が冬のときは同様に北半球は夏となる。 社会通念・気象学では1月・2月・12月。たとえば「暖冬」「厳冬」などはこの3か月の平均気温で判断する。 寒候年・1年間の間で1月、2月、12月とすると1シーズンとしての冬を評価できない。そのため1月、2月を含む年をそのシーズンで括る。たとえば、「2009年の冬」といった場合、2008年の12月、2009年の1月、2月である。また、「2008/2009年冬」という書き方をする。初雪・終雪の日など11月以前、3月以降になることのあるようなものもこの定義による。 二十四節気に基づく節切りでは立冬から立春の前日まで。 旧暦による月切りでは十月・十一月・十二月。上に近いが、最大半月ずれる。 年度では1月・2月・3月。英語ではこの3か月をwinter quarterと呼ぶ。 天文学上は冬至から春分まで。ここでの「冬至」「春...
Read more

浄心駅

Image
浄心駅 浄心駅5番出口（2010年3月） じょうしん Joshin ◄ T03 庄内通 (1.4km) (0.8km) 浅間町 T05 ► 所在地 名古屋市西区城西四丁目3208 愛知県の地図を表示 名古屋市の地図を表示 北緯35度11分32秒 東経136度53分27秒 駅番号 ○ T04 所属事業者 名古屋市交通局 （名古屋市営地下鉄） 所属路線 鶴舞線 [1] キロ程 4.1km（上小田井起点） 駅構造 地下駅 ホーム 2面2線 乗車人員 -統計年度- 7,116人/日（降車客含まず） -2017年- 開業年月日 1981年（昭和56年）11月27日 [1] テンプレートを表示 浄心駅 （じょうしんえき）は、愛知県名古屋市西区城西4丁目にある、名古屋市営地下鉄鶴舞線の駅である。駅番号は T04 。 運行上の拠点であり乗務員の交代が当駅で行われる他、上り最終電車のみ当駅止まりとなる（翌朝当駅から上小田井駅へ回送し、上小田井駅発の列車となる）。かつては日中にも当駅起終点の列車が1往復設定されていた。 目次 1 歴史 2 駅構造 2.1 のりば 3 駅周辺 4 バス路線 5 隣の駅 6 脚注 7 関連項目 8 外部リンク 歴史 1981年（昭和56年）11月27日 - 当駅 - 伏見間の延伸に際し開業 [1] 。 1984年（昭和59年）9月6日 - 庄内緑地公園 - 当駅間の開業に伴い途中駅となる [1] 。 駅構造 浄心駅ホーム 相対式ホーム2面2線を有する地下駅。1番ホームには東改札口、2番ホームには西改札口がそれぞれあり、両ホームは線路の下を通る連絡通路でつながっている。改札外では東西それぞれのコンコースをつなぐ通路は無く、分断されている。 1番又は2番出入り口から入り階段を降りると1番ホーム（赤池・豊田市方面）にしか行けず、4～6番出入り口から入り階段を降りると2番ホーム（上小田井・犬山方面）にしか行くことができない。 よって、例えば2番ホームで降りて...
Read more

カンタス航空

Image
カンタス航空 Qantas Airways IATA QF [1] ICAO QFA コールサイン Qantas 法人番号 1700150004605 設立 1920年 ハブ空港 キングスフォード・スミス国際空港 メルボルン空港 焦点空港 香港国際空港 シンガポール・チャンギ国際空港 パース空港 ブリスベン空港 アデレード空港 マイレージサービス Frequent Flyer 会員ラウンジ Qantas Club 航空連合 ワンワールド 保有機材数 213機 (147機発注中) 就航地 144都市 (39カ国) 親会社 Qantas Airways Limited 本拠地 オーストラリア ニューサウスウェールズ州シドニー 代表者 Alan Joyce (CEO) Leigh Clifford (会長) 外部リンク qantas.com テンプレートを表示 カンタス航空本社 (Qantas Building A) カンタス航空 （カンタスこうくう、英語: Qantas Airways Limited ）は、オーストラリアおよび南半球最大手の航空会社。 オーストラリアでのQantasの発音は、 Quantas ( [ˈkwɒntəs] [2] [3] [4] 、 クウォンタス ) のように発音される。 目次 1 概要 2 歴史 2.1 設立 2.2 第二次世界大戦 2.3 第二次世界大戦後 2.4 拡大 2.5 現在 3 就航都市 4 保有機材 4.1 特別塗装機 5 マイレージサービス 6 機内サービス 6.1 広報活動 6.2 新ユニフォーム 7 事故及び故障 8 「オーストラリア・アジア航空」 9 補足 10 関連項目 11 脚注 12 外部リンク 概要 カンタス航空はオーストラリアのナショナルフラッグの航空会社であり、その機材数、国際便と国内便の就航都市数...
Read more