Jfyhkgu

Криптографические обозначения, используемые в протоколах проверки подлинности и обмена ключами

A{displaystyle A}	Идентификаторы Алисы (Alice), инициатора сессии
B{displaystyle B}	Идентификатор Боба (Bob), стороны, с которой устанавливается сессия
T{displaystyle T}	Идентификатор Трента (Trent), доверенной промежуточной стороны
KA,KB,KT{displaystyle K_{A},K_{B},K_{T}}	Открытые ключи Алисы, Боба и Трента
KA−1,KB−1,KT−1{displaystyle K_{A}^{-1},K_{B}^{-1},K_{T}^{-1}}	Секретные ключи Алисы, Боба и Трента
EA,{...}KA{displaystyle E_{A},left{...right}_{K_{A}}}	Шифрование данных ключом Алисы, либо совместным ключом Алисы и Трента
EB,{...}KB{displaystyle E_{B},left{...right}_{K_{B}}}	Шифрование данных ключом Боба, либо совместным ключом Боба и Трента
{...}KB−1,{...}KA−1{displaystyle left{...right}_{K_{B}^{-1}},left{...right}_{K_{A}^{-1}}}	Шифрование данных секретными ключами Алисы, Боба (цифровая подпись)
I{displaystyle I}	Порядковый номер сессии (для предотвращения атаки с повтором)
K{displaystyle K}	Случайный сеансовый ключ, который будет использоваться для симметричного шифрования данных
EK,{...}K{displaystyle E_{K},left{...right}_{K}}	Шифрование данных временным сеансовым ключом
TA,TB{displaystyle T_{A},T_{B}}	Метки времени, добавляемые в сообщения Алисой и Бобом соответственно
RA,RB{displaystyle R_{A},R_{B}}	Случайные числа (nonce), которые были выбраны Алисой и Бобом соответственно

Протокол Нидхема — Шрёдера — общее название для симметричного и асимметричного протоколов аутентификации и обмена ключами. Оба протокола были предложены Майклом Шрёдером (англ.)русск. и Роджером Нидхемом^[1]. Вариант, основанный на симметричном шифровании, использует промежуточную доверенную сторону. Этот протокол стал основой для целого класса подобных протоколов. Например, Kerberos является одним из вариантов симметричного протокола Нидхема — Шрёдера. Вариант, основанный на асимметричном шифровании, предназначен для взаимной аутентификации сторон. В оригинальном виде оба варианта протокола являются уязвимыми^[2][3].

История |

Протокол для аутентификации с симметричным ключом, вероятно являющийся самым знаменитым протоколом аутентификации и установления ключа, был сформулирован Майклом Шрёдером и Роджером Нидхемом в 1978 году^[1]. Однако, он уязвим для атаки, изобретенной Дороти Деннинг (англ. Dorothy E. Denning) и Джованни Марией Сакко (англ. Giovanni Maria Sacco) в 1981 году^[2]. Несмотря на это, он стал основой для целого класса подобных протоколов. В частности, протокол Kerberos является одним из вариантов Нидхем-Шрёдер-протокола аутентификации на основе доверенной третьей стороны и его модификациях, предложенных Деннинг и Сакко^[2]. Протокол Нидхема-Шрёдера для аутентификации с открытым ключом также является уязвимым. В 1995 году Лоу (англ. Gavin Lowe) описал возможную атаку на протокол^[3].

Протокол Нидхема-Шрёдера для аутентификации с симметричным ключом |

Протокол Нидхема-Шрёдера для аутентификации с симметричным ключом

При схеме шифрования с симметричным ключом, предполагается, что секретный ключ известен и серверу аутентификации T{displaystyle T} (Трент) и обоим субъектам обмена: A{displaystyle A} (Алиса) и B{displaystyle B} (Боб). Изначально оба субъекта имеют секретные ключи: KA{displaystyle K_{A}} и KB{displaystyle K_{B}}, известные только им и некоторой доверенной стороне — серверу аутентификации. В ходе выполнения протокола Алиса и Боб получают от сервера новый секретный сессионный ключ для шифрования взаимных сообщений в данном сеансе связи, то есть сообщения от Алисы к Бобу расшифровать может только Боб, сообщения от Боба к Алисе расшифровать может только Алиса. Кроме того субъекты обмена должны быть уверены, что пришедшее сообщение было отправлено именно тем, с кем должен произойти обмен. Боб должен быть уверен, что получил сообщение именно от Алисы и наоборот. Это также обеспечивается протоколом. Предположим, что обмен инициирует Алиса. Будем полагать, что сервер аутентификации у них общий. Рассмотрим реализацию протокола^[4]:

1. Alice→A,B,RA→Trent{displaystyle Aliceto A,B,R_{A}to Trent}


2. Trent→{RA,B,K,{K,A}KB}KA→Alice{displaystyle Trentto left{R_{A},B,K,left{K,Aright}_{K_{B}}right}_{K_{A}}to Alice}


3. Alice→{K,A}KB→Bob{displaystyle Aliceto left{K,Aright}_{K_{B}}to Bob}


4. Bob→{RB}K→Alice{displaystyle Bobto left{R_{B}right}_{K}to Alice}


5. Alice→{RB−1}K→Bob{displaystyle Aliceto left{R_{B}-1right}_{K}to Bob}

Обмен начинается с того, что Алиса генерирует некоторое случайное число RA{displaystyle R_{A}} (идентификатор), использующееся один раз. Первое сообщение от Алисы к Тренту содержит в себе имена участников предстоящего обмена и генерированное Алисой случайное число:

Alice→A,B,RA→Trent{displaystyle Aliceto A,B,R_{A}to Trent}

Данное сообщение посылается открытым текстом, но может быть зашифровано ключом Алисы KA{displaystyle K_{A}}:

Alice→{A,B,RA}KA→Trent{displaystyle Aliceto left{A,B,R_{A}right}_{K_{A}}to Trent}

При получении этого сообщения Трент извлекает из базы данных секретные ключи Алисы и Боба: KA{displaystyle K_{A}} и KB{displaystyle K_{B}}, а также вычисляет новый сессионный ключ K{displaystyle K}. Далее Трент посылает Алисе следующее сообщение:

Trent→{RA,B,K,{K,A}KB}KA→Alice{displaystyle Trentto left{R_{A},B,K,left{K,Aright}_{K_{B}}right}_{K_{A}}to Alice}

Алиса может расшифровать и прочесть сообщение от Трента. Она проверяет наличие своего идентификатора RA{displaystyle R_{A}} в сообщении, что подтверждает то, что данное сообщение является откликом на её первое сообщение Тренту. Также она проверяет имя субъекта, с которым собирается обмениваться данными. Эта проверка обязательна, так как если бы не было этого имени, Злоумышленник мог бы заменить имя Боба на своё в первом сообщении, и Алиса, ничего не подозревая, в дальнейшем бы взаимодействовала со Злоумышленником. Часть сообщения Алиса прочитать не может, так как эта часть зашифрована ключом Боба. Алиса пересылает Бобу зашифрованный его ключом фрагмент:

Alice→{K,A}KB→Bob{displaystyle Aliceto left{K,Aright}_{K_{B}}to Bob}

Расшифровать его может только Боб, так как оно зашифровано его секретным ключом. После расшифровки Боб тоже владеет сессионным ключом K{displaystyle K}. Имя Алисы в сообщении подтверждает факт, что сообщение от неё. Далее при обмене данными будет использоваться сессионный ключ. Чтобы сделать схему симметричной и уменьшить вероятность атаки воспроизведения, Боб генерирует некоторое случайное число RB{displaystyle R_{B}} (идентификатор Боба) и посылает Алисе следующее сообщение, зашифрованное сессионным ключом:

Bob→{RB}K→Alice{displaystyle Bobto left{R_{B}right}_{K}to Alice}

Алиса расшифрует его и посылает отклик, который ожидает Боб, также зашифрованный сессионным ключом:

Alice→{RB−1}K→Bob{displaystyle Aliceto left{R_{B}-1right}_{K}to Bob}

Для регулярно взаимодействующих партнёров можно сократить число сообщений до трёх, убрав первые два. При этом ключ будет использоваться многократно^[5].

Атака на протокол Нидхема-Шрёдера для аутентификации с симметричным ключом |

Атака на протокол Нидхема-Шрёдера для аутентификации с симметричным ключом

Протокол Нидхема-Шрёдера уязвим для атаки с повторной передачей сообщения, изобретённой Дороти Деннинг (англ. Dorothy E. Denning) и Джованни Марией Сакко (англ. Giovanni Maria Sacco) в 1981 году^[2]. В ходе атаки Злоумышленник перехватывает и заменяет сообщения из пунктов 3,4,5 протокола. Злоумышленник перехватывает сообщение от Алисы к Бобу на третьем шаге протокола и блокирует Алису. Потом заменяет актуальное сообщение Алисы на другое из старого сеанса между Алисой и Бобом. Исходя из предположения об уязвимости старого сеансового ключа, Злоумышленник может узнать его значение и начать обмен данными с Бобом под видом Алисы^[4].

В результате Боб думает, что имеет новый сеансовый ключ с Алисой, но на самом деле ключ старый и известен Злоумышленнику.

Рассмотрим возможную реализацию атаки:

• Обмен начинается так же, как и в протоколе. Алиса генерирует случайное число и посылает Тренту. Трент извлекает из базы данных секретные ключи Алисы и Боба, вычисляет новый сессионный ключ K{displaystyle K} и посылает ответ Алисе. Алиса расшифровывает сообщение, проверяет случайное число и имя субъекта, с которым собирается обмениваться данными. Отправляет сообщение Бобу.

Alice→A,B,RA→Trent{displaystyle Aliceto A,B,R_{A}to Trent}

Trent→{RA,B,K,{K,A}KB}KA→Alice{displaystyle Trentto left{R_{A},B,K,left{K,Aright}_{K_{B}}right}_{K_{A}}to Alice}

Alice→{K,A}KB→Bob{displaystyle Aliceto left{K,Aright}_{K_{B}}to Bob}

• После этого в ход протокола вмешивается Злоумышленник. Сначала он перехватывает сообщение Алисы Бобу, потом полностью блокирует канал связи Алисы. Исходя из предположения об уязвимости старого сеансового ключа, Злоумышленник может узнать его значение. Кроме значения старого ключа у Злоумышленника есть материал старого сеанса между Алисой и Бобом: Alice→{KP,A}KB→Bob{displaystyle Aliceto left{K_{P},Aright}_{K_{B}}to Bob}, где KP{displaystyle K_{P}} (previous key) — старый ключ. Выдавая себя за Алису, он посылает Бобу сообщение со старым ключом:

Alice(Attacker)→{KP,A}KB→Bob{displaystyle Alice(Attacker)to left{K_{P},Aright}_{K_{B}}to Bob}

• Боб расшифровывает сообщение и убеждается, что оно от Алисы, не подозревая, что подвергся атаке и общается уже со Злоумышленником. Он посылает «Алисе» своё случайное число:

Bob→{RB}KP→Alice(Attacker){displaystyle Bobto left{R_{B}right}_{K_{P}}to Alice(Attacker)}

• Злоумышленник, зная значение старого ключа, расшифровывает сообщение Боба. Он, как и положено, уменьшает на единицу значение случайного числа Боба, шифрует результат с помощью того же старого сессионного ключа и отправляет сообщение Бобу:

Alice(Attacker)→{RB−1}KP→Bob{displaystyle Alice(Attacker)to left{R_{B}-1right}_{K_{P}}to Bob}

В итоге Боб уверен, что установил сеанс связи с Алисой, так как все необходимые шаги протокола были проделаны верно и все сообщения оказались корректны.

Эта атака порождает более серьёзную опасность — отсутствие реальной связи между партнёрами. Злоумышленник не обязан ждать, когда Алиса запустит протокол. Поскольку он знает старый сеансовый ключ KP{displaystyle K_{P}}, он может сам начать атаку, начав протокол с этапа 3. Боб будет думать, что установил контакт с Алисой в то время как Алиса вообще не выходила на связь^[6].

Исправление уязвимости |

Деннинг и Сакко предложили использовать метки времени в сообщениях для предотвращения атак, подобных рассмотренной выше^[2]. Обозначим такую метку буквой t{displaystyle t}. Рассмотрим вариант исправления уязвимости:

1. Alice→A,B,RA→Trent{displaystyle Aliceto A,B,R_{A}to Trent}


2. 
   Trent→{RA,A,B,{K}KA}KA{displaystyle Trentto left{R_{A},A,B,left{Kright}_{K_{A}}right}_{K_{A}}}, {t,A,B,{K}KB}KB→Alice{displaystyle left{t,A,B,left{Kright}_{K_{B}}right}_{K_{B}}to Alice}
   


3. Alice→{t,A,B,{K}KB}KB→Bob{displaystyle Aliceto left{t,A,B,left{Kright}_{K_{B}}right}_{K_{B}}to Bob}


4. Bob→{RB}K→Alice{displaystyle Bobto left{R_{B}right}_{K}to Alice}


5. Alice→{RB−1}K→Bob{displaystyle Aliceto left{R_{B}-1right}_{K}to Bob}

Получив протокольные сообщения от Трента, Алиса и Боб могут обнаружить, что их послания остались без ответа, проверив неравенство:

tcurr−t<Δt1+Δt2{displaystyle t_{curr}-t<Delta t_{1}+Delta t_{2}}

где tcurr{displaystyle t_{curr}} (current time) — текущее локальное время получателя; Δt1{displaystyle Delta t_{1}} — интервал, представляющий допустимую разницу между временем Трента и локальным временем; Δt2{displaystyle Delta t_{2}} — ожидаемая временная задержка. Отсюда они убеждаются в «свежести» сообщений и в частности сессионного ключа. Так как временная метка зашифрована секретными ключами Алисы и Боба, то в идеальной схеме шифрования имитация Трента невозможна^[7].

Также в данной уточнённой спецификации протокола необходимость защиты целостности данных выделена явно. Если сообщения, которыми обмениваются участники протокола, не искажались в процессе передачи, то после процедуры верификации обе стороны могут быть уверены, что сеансовый ключ согласован как с пользователями, так и с идентификатором «свежести». Это должно убедить их в подлинности друг друга и в том, что не используется старый сеансовый ключ^[8].

Случай разных серверов аутентификации |

Случай разных серверов аутентификации

В реальной жизни Алиса и Боб могут оказаться на достаточно большом расстоянии, чтобы не существовало общего сервера аутентификации^[5]. По этой причине в общем случае Алиса может иметь свой сервер аутентификации: TA{displaystyle T_{A}}, а Боб свой: TB{displaystyle T_{B}}. Так как и в этом случае перед Алисой стоит задача построить для Боба сообщение вида {K,A}KB{displaystyle left{K,Aright}_{K_{B}}}. Для его формирования будут задействованы оба сервера, так как только TA{displaystyle T_{A}} умеет шифровать ключом Алисы KA{displaystyle K_{A}}, и только TB{displaystyle T_{B}} может использовать ключ Боба: KB{displaystyle K_{B}}. При этом безопасность обмена между серверами предполагается обеспеченной. Рассмотрим пример для случая двух разных серверов, имеющих соединение друг с другом:

1. Alice→A,B,RA→TrentA{displaystyle Aliceto A,B,R_{A}to Trent_{A}}


2. TrentA→A,B,RA,K→TrentB{displaystyle Trent_{A}to A,B,R_{A},Kto Trent_{B}}


3. TrentB→A,RA,{K,A}KB→TrentA{displaystyle Trent_{B}to A,R_{A},left{K,Aright}_{K_{B}}to Trent_{A}}


4. TrentA→{RA,B,K,{K,A}KB}KA→Alice{displaystyle Trent_{A}to left{R_{A},B,K,left{K,Aright}_{K_{B}}right}_{K_{A}}to Alice}


5. Alice→{K,A}KB→Bob{displaystyle Aliceto left{K,Aright}_{K_{B}}to Bob}


6. Bob→{RB}K→Alice{displaystyle Bobto left{R_{B}right}_{K}to Alice}


7. Alice→{RB−1}K→Bob{displaystyle Aliceto left{R_{B}-1right}_{K}to Bob}

Шаги 1, 4-7 соответствуют шагам 1-5 из описанного выше случая с общим сервером аутентификации. На втором шаге сервер Алисы, не найдя в списке своих клиентов Боба, обращается к серверу Боба. Тот знает ключ Боба и может выполнить необходимое шифрование. После чего зашифрованная информация передается обратно серверу аутентификации Алисы, который и посылает её Алисе^[5].

Протокол с аутентификацией сущности |

Механизм «отклика-отзыва»^[9] из протокола обеспечивает так называемую аутентификацию сущности (entity authentication)^{[ISO 1]}. Аутентификация сущности осуществляется с помощью проверки верифицирующим пользователем некоторой криптографической операции. В её ходе демонстрируется существование доказывающего пользователя, которое считается подтверждённым, если доказывающий пользователь выполнил некоторую криптографическую операцию после события, которое другой пользователь считает последним.

На втором этапе протокола Нидхема-Шрёдера Алиса расшифровывает одноразовое случайное число, которое сгенерировала она сама на первом этапе. Это подтверждает тот факт, что Трент выполнил шифрование после получения сообщения от Алисы. В итоге Алиса знает, что Трент существовал после этого события, то есть Трент прошел аутентификацию существования по отношению к Алисе. В то же время Боб, участвующий в том же протоколе, не может быть уверен в существовании Трента^[7].

Протокол Нидхема-Шрёдера для аутентификации с открытым ключом |

Криптосистемы с открытым ключом |

Введём обозначения:

• 
  KA{displaystyle K_{A}} — открытый ключ Алисы;


• 
  KA−1{displaystyle K_{A}^{-1}} — секретный ключ Алисы.

Причем секретный ключ знает только Алиса, а открытый ключ известен окружающим.

• 
  M{displaystyle M} — открытый текст;


• 
  {M}KA{displaystyle left{Mright}_{K_{A}}} — текст зашифрован открытым ключом Алисы и может быть расшифрован только Алисой с помощью её секретного ключа;


• 
  {M}KA−1{displaystyle left{Mright}_{K_{A}^{-1}}} — текст зашифрован секретным ключом Алисы и может быть расшифрован с помощью открытого ключа Алисы.

Это означает, что текст {M}KA−1{displaystyle left{Mright}_{K_{A}^{-1}}} при идеальном шифровании гарантированно создан Алисой, потому что данным секретным ключом владеет только она. Именно поэтому зашифрованный текст {M}KA−1{displaystyle left{Mright}_{K_{A}^{-1}}} называется цифровой подписью сообщения M{displaystyle M}. Его расшифровка с помощью открытого ключа называется верификацией подписи Алисы^[10].

Протокол Нидхема-Шрёдера для аутентификации с открытым ключом |

Протокол Нидхема — Шрёдера для аутентификации с открытым ключом

Асимметричный вариант (двух ключевая схема) протокола Нидхема — Шрёдера. Трент владеет открытыми ключами всех обслуживаемых им клиентов. Алиса имеет открытый ключ KA{displaystyle K_{A}} и секретный ключ KA−1{displaystyle K_{A}^{-1}}, Боб — KB{displaystyle K_{B}} и KB−1{displaystyle K_{B}^{-1}}, Трент — KT{displaystyle K_{T}} и KT−1{displaystyle K_{T}^{-1}}. Пусть Алиса инициирует новый сеанс связи с Бобом^[11]:

1. Alice→A,B→Trent{displaystyle Aliceto A,Bto Trent}


2. Trent→{KB,B}KT−1→Alice{displaystyle Trentto {left{K_{B},Bright}}_{K_{T}^{-1}}to Alice}


3. Alice→T,{RA,A}KB→Bob{displaystyle Aliceto T,left{R_{A},Aright}_{K_{B}}to Bob}


4. Bob→B,A→Trent{displaystyle Bobto B,Ato Trent}


5. Trent→{KA,A}KT−1→Bob{displaystyle Trentto left{K_{A},Aright}_{K_{T}^{-1}}to Bob}


6. Bob→{RA,RB}KA→Alice{displaystyle Bobto left{R_{A},R_{B}right}_{K_{A}}to Alice}


7. Alice→{RB}KB→Bob{displaystyle Aliceto left{R_{B}right}_{K_{B}}to Bob}

Алиса — инициатор протокола — в первом сообщении запрашивает у Трента открытый ключ Боба:

Alice→A,B→Trent{displaystyle Aliceto A,Bto Trent}

На что Трент на втором этапе протокола отвечает сообщением с открытым ключом Боба и его именем. Сообщение зашифровано секретным ключом Трента, то есть является его цифровой подписью. Эта подпись должна убедить Алису, что она получила сообщение именно от Трента. Предполагается, что Алиса знает открытый ключ Трента и способна расшифровать сообщение, то есть верифицировать подпись.

Trent→{KB,B}KT−1→Alice{displaystyle Trentto {left{K_{B},Bright}}_{K_{T}^{-1}}to Alice}

Далее Алиса генерирует случайное число RA{displaystyle R_{A}} и вместе со своим именем отправляет Бобу, предварительно зашифровав открытым ключом Боба.

Alice→T,{RA,A}KB→Bob{displaystyle Aliceto T,left{R_{A},Aright}_{K_{B}}to Bob}

Только Боб может расшифровать данное сообщение, так как для этого необходим его секретный ключ KB−1{displaystyle K_{B}^{-1}}. Из сообщения он узнаёт, что Алиса хочет начать обмен данными с ним. Следовательно, Бобу нужен открытый ключ Алисы и он делает операции, аналогичные проделанным Алисой:

Bob→B,A→Trent{displaystyle Bobto B,Ato Trent}

Trent→{KA,A}KT−1→Bob{displaystyle Trentto left{K_{A},Aright}_{K_{T}^{-1}}to Bob}

В результате участники обмена знают открытые ключи друг друга. После этого производится взаимная аутентификация с помощью генерированных случайных чисел:

Bob→{RA,RB}KA→Alice{displaystyle Bobto left{R_{A},R_{B}right}_{K_{A}}to Alice}

Alice→{RB}KB→Bob{displaystyle Aliceto left{R_{B}right}_{K_{B}}to Bob}

Нидхем и Шрёдер предложили использовать числа RA{displaystyle R_{A}} и RB{displaystyle R_{B}} для инициализации общего секретного ключа^[1], обеспечивающего секретную связь между Алисой и Бобом. Позже Деннинг и Сакко указали, что этот протокол не гарантирует, что открытые ключи являются новыми, а не повторами старых. Эту проблему можно решить разными способами, в частности используя временные метки^[2] в сообщениях с ключами. Нидхем и Шрёдер также рассматривали возможность применения меток времени, но отвергли эту идею из-за отсутствия качественного эталона времени^[12].

Атака на протокол Нидхема-Шрёдера для аутентификации с открытым ключом |

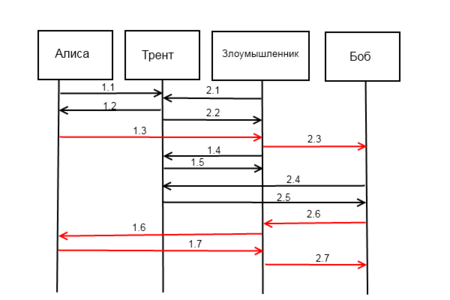
Атака на протокол Нидхема-Шрёдера для аутентификации с открытым ключом

Атака на протокол была предложена Лоу (англ. Gavin Lowe)^[3]. Он разделил протокол на две части, не связанные логически. Первая: 1, 2, 4, 5 этапы протокола — получение открытого ключа. Вторая: 3, 6, 7 этапы — аутентификация Алисы и Боба. Будем полагать, что первая часть состоялась и рассмотрим вторую:

3. Alice→T,{RA,A}KB→Bob{displaystyle Aliceto T,left{R_{A},Aright}_{K_{B}}to Bob}

6. Bob→{RA,RB}KA→Alice{displaystyle Bobto left{R_{A},R_{B}right}_{K_{A}}to Alice}

7. Alice→{RB}KB→Bob{displaystyle Aliceto left{R_{B}right}_{K_{B}}to Bob}

Пусть Злоумышленник (Аttacker) — лицо, являющееся законным пользователем системы. Он может проводить стандартные сеансы связи с остальными пользователями системы. Для атаки используется одновременный запуск двух протоколов: в первом Алиса проводит корректный сеанс со Злоумышленником, во втором Злоумышленник выдаёт себя за Алису при общении с Бобом^[13].

1.3. Alice→T,{RA,A}KAt→Attacker{displaystyle Aliceto T,left{R_{A},Aright}_{K_{At}}to Attacker}

2.3. Attacker(Alice)→T,{RA,A}KB→Bob{displaystyle Attacker(Alice)to T,left{R_{A},Aright}_{K_{B}}to Bob}

2.6. Bob→{RA,RB}KA→Attacker(Alice){displaystyle Bobto left{R_{A},R_{B}right}_{K_{A}}to Attacker(Alice)}

1.6. Attacker→{RA,RB}KA→Alice{displaystyle Attackerto left{R_{A},R_{B}right}_{K_{A}}to Alice}

1.7. Alice→{RB}KAt→Attacker{displaystyle Aliceto left{R_{B}right}_{K_{At}}to Attacker}

2.7. Attacker(Alice)→{RB}KB→Bob{displaystyle Attacker(Alice)to left{R_{B}right}_{K_{B}}to Bob}

На этапе 1.3 Алиса посылает Злоумышленнику случайное число RA{displaystyle R_{A}}, которое Злоумышленник тут же на этапе 2.3 другого протокола пересылает Бобу. Боб принимает это сообщение и на этапе 2.6 генерирует своё случайное число и отвечает, по его мнению, Алисе. Злоумышленник не может расшифровать это сообщение, поэтому он на этапе 1.6 пересылает его Алисе. Алиса получает сообщение, не вызывающее подозрений, расшифровывает и возвращает на этапе 1.7 Злоумышленнику случайное число Боба, зашифровав сообщение открытым ключом Злоумышленника. Теперь Злоумышленник знает случайное число Боба и может ответить ему на этапе 2.7. Боб уверен, что установил сеанс связи с Алисой, так как шифровал сообщение со случайным числом её ключом и получил правильный ответ.

Ключевой момент атаки состоит в том, что Злоумышленник может заставить Алису расшифровать для него случайное число Боба. Алиса в данной атаке выступает оракулом — пользователем системы, который выполняет некоторую криптографическую операцию в интересах Злоумышленника^[14].

Пример последствий |

Рассмотрим пример последствий данной атаки. Пусть Боб — это некоторый банк. Тогда Злоумышленник, выдав себя за Алису, может воспользоваться её счетом и перевести с него деньги на свой. Банк будет уверен, что операция была выполнена Алисой^[14].

Простое исправление протокола |

Для предотвращения атаки, описанной выше, необходимо на шестом этапе добавить в сообщение имя отвечающего:

2.6. Bob→{B,RA,RB}KA→Attacker(Alice){displaystyle Bobto left{B,R_{A},R_{B}right}_{K_{A}}to Attacker(Alice)}

В этом случае Злоумышленник не сможет переслать сообщение Алисе, так как Алиса будет ждать от него соответственно следующее сообщение:

1.6. Attacker→{At,RA,RB}KA→Alice{displaystyle Attackerto left{At,R_{A},R_{B}right}_{K_{A}}to Alice}

которое Злоумышленник не может получить ни пересылками сообщений Боба, ни собственными силами^[14].

Исправление уязвимости |

Первый вариант |

3. Alice→{{RA,A}KA−1}KB→Bob{displaystyle Aliceto left{left{R_{A},Aright}_{K_{A}^{-1}}right}_{K_{B}}to Bob}

6. Bob→{RA,{RB}KB−1}KA→Alice{displaystyle Bobto left{R_{A},left{R_{B}right}_{K_{B}^{-1}}right}_{K_{A}}to Alice}

7. Alice→{{RB}KA−1}KB→Bob{displaystyle Aliceto left{left{R_{B}right}_{K_{A}^{-1}}right}_{K_{B}}to Bob}

В уточнённой спецификации {RA,A}KA−1{displaystyle left{R_{A},Aright}_{K_{A}^{-1}}} — это сообщение, для верификации которого необходимо использовать открытый ключ Алисы, то есть это подпись Алисы. В этой спецификации случайные числа сначала подписываются, а потом шифруются открытым ключом другого пользователя. Из-за того, что на этапе 6 Боб подписывает своё число, атака Лоу становится невозможной. Если Злоумышленник перешлёт сообщение Алисе, то она заметит ошибку при верификации^[15].

Второй вариант |

С помощью метода «зашифруй и подпиши» можно уточнить следующим образом:

3. Alice→{{RA}KB,A}KA−1→Bob{displaystyle Aliceto left{left{R_{A}right}_{K_{B}},Aright}_{K_{A}^{-1}}to Bob}

6. Bob→{{RA,RB}KA}KB−1→Alice{displaystyle Bobto left{left{R_{A},R_{B}right}_{K_{A}}right}_{K_{B}^{-1}}to Alice}

7. Alice→{{RB}KB}KA−1→Bob{displaystyle Aliceto left{left{R_{B}right}_{K_{B}}right}_{K_{A}^{-1}}to Bob}

Теперь Злоумышленник даже не в состоянии запустить протокол связи с Бобом от имени другого лица^[15].

Практическое использование |

Для решения проблемы аутентификации сетевых пользователей предназначен протокол Kerberos. Его основная идея заключается в использовании доверенной третьей стороны, предоставляющей пользователю доступ к серверу с помощью общего сеансового ключа, разделённого между пользователем и сервером. В основе данного протокола лежит вариант протокола Нидхема — Шрёдера с использованием временной метки^[16][1].

Примечания |

Стандарты |

Литература |

• Roger M. Needham, Michael D. Schroeder. Using encryption for authentication in large networks of computers (англ.) // Commun. ACM. — New York, NY, USA: ACM, 1978. — Vol. 21, iss. 12. — P. 993—999. — ISSN 0001-0782. — DOI:10.1145/359657.359659.


• Dorothy E. Denning, Giovanni Maria Sacco. Timestamps in key distribution protocols (англ.) // Commun. ACM. — New York, NY, USA: ACM, 1981. — Vol. 24, iss. Aug, 1981, no. 8. — P. 533—536. — ISSN 0001-0782. — DOI:10.1145/358722.358740.


• Roger M. Needham, Michael D. Schroeder. Authentication revisited (англ.) // SIGOPS Oper. Syst. Rev.. — New York, NY, USA: ACM, 1987. — Vol. 21, iss. 1. — P. 7—7. — ISSN 0163-5980. — DOI:10.1145/24592.24593.


• Gavin Lowe. An attack on the Needham-Schroeder public-key authentication protocol (англ.) // Information Processing Letters. — 1995. — Vol. 56, no. 3. — P. 131—133. — ISSN 0020-0190. — DOI:10.1016/0020-0190(95)00144-2.


• Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.


• Венбо Мао. Современная криптография: теория и практика = Modern Cryptography: Theory and Practice. — Издательский дом "Вильямс", 2005. — ISBN 5-8459-0847-7.


• Семенов Ю.А. Протокол аутентификации Нидхема-Шрёдера в случаях симметричной и асимметричной системы шифрования (рус.). Проверено 8 декабря 2012. Архивировано 8 декабря 2012 года.

Ссылки |

• Needham-Schroeder Public Key (англ.). Проверено 2 августа 2010. Архивировано 6 декабря 2012 года.


• Symmetric-key protocol (англ.). Проверено 17 ноября 2012. Архивировано 6 декабря 2012 года.


• The public-key protocol amended by Lowe (англ.). Проверено 17 ноября 2012. Архивировано 6 декабря 2012 года.

Эта статья входит в число хороших статей русскоязычного раздела Википедии.