Jfyhkgu

Teoría de la Relatividad, parte de Walk of Ideas, en la Isla de los Museos (Berlín). Festejando el Año mundial de la física 2005 en el centenario de la publicación de la ecuación más famosa del mundo.

La teoría de la relatividad especial, también llamada teoría de la relatividad restringida, es una teoría de la física publicada en 1905 por Albert Einstein.^[1]​ Surge de la observación de que la velocidad de la luz en el vacío es igual en todos los sistemas de referencia inerciales y de obtener todas las consecuencias del principio de relatividad de Galileo, según él, cualquier experimento realizado, en un sistema de referencia inercial, se desarrollará de manera idéntica en cualquier otro sistema inercial.

La teoría es "especial", ya que sólo se aplica en el caso especial donde la curvatura del espacio-tiempo debido a la gravedad es despreciable.^[2]​^[3]​ Con el fin de incluir la gravedad, Einstein formuló la relatividad general en 1915. La relatividad general es capaz de manejar marcos de referencia acelerados, algo que no era posible con las teorías anteriores.^[4]​

La Teoría de la relatividad especial estableció nuevas ecuaciones que facilitan pasar de un sistema de referencia inercial a otro. Las ecuaciones correspondientes conducen a fenómenos que chocan con el sentido común, como son la contracción espacial, la dilatación del tiempo, un límite universal a la velocidad, la equivalencia entre masa y energía o la relatividad de la simultaneidad entre otros, siendo la fórmula E=mc² o la paradoja de los gemelos dos de los ejemplos más conocidos.^[5]​

La relatividad especial tuvo también un impacto en la filosofía, eliminando toda posibilidad de existencia de un tiempo y de un espacio absoluto en el conjunto del universo.

Historia

A finales del siglo XIX los físicos pensaban que la mecánica clásica de Newton, basada en la llamada relatividad de Galileo Galilei (origen de las ecuaciones matemáticas conocidas como transformaciones de Galileo), describía los conceptos de velocidad y fuerza para todos los observadores (o sistemas de referencia). Sin embargo, Hendrik Lorentz y un poco antes Woldemar Voigt habían comprobado que las ecuaciones de Maxwell, que gobiernan el electromagnetismo, no cumplían las transformaciones de Galileo cuando el sistema de referencia inercial varía (por ejemplo, cuando se considera el mismo problema físico desde el punto de vista de dos observadores que se mueven uno respecto del otro). En particular las ecuaciones de Maxwell parecían requerir que la velocidad de la luz fuera constante (razón por la que se interpretó que esa velocidad se refería a la velocidad de la luz respecto al éter). Sin embargo, el experimento de Michelson y Morley sirvió para confirmar que la velocidad de la luz permanecía constante para cualquier velocidad y movimiento relativo al supuesto éter omnipresente y, además, independientemente del sistema de referencia en el cual se medía (contrariamente a lo esperado de aplicar las transformaciones de Galileo) .^[6]​ Por tanto la hipótesis del éter quedaba descartada y se abría un problema teórico grave asociado a las transformaciones de Galileo. Hendrik Lorentz ya había encontrado que las transformaciones correctas que garantizaban la invariancia no eran las de Galileo, sino las que actualmente se conocen como transformaciones de Lorentz.

Durante años las transformaciones de Lorentz y los trabajos de Henri Poincaré sobre el tema quedaron inexplicados hasta que Albert Einstein, un físico desconocido hasta 1905, sería capaz de darles una interpretación considerando el carácter relativo del tiempo y el espacio. Einstein también había sido influido por el físico y filósofo Ernst Mach.^[7]​ Einstein leyó a Ernst Mach cuando era estudiante y ya era seguidor suyo en 1902, cuando vivía en Zúrich y se reunía regularmente con sus amigos Conrad Habicht y Maurice Solovine (Véase Academia Olimpia).^[8]​ Einstein insistió para que el grupo leyese los dos libros que Mach había publicado hasta esa fecha: El desarrollo de la mecánica (título original, Die Mechanik in ihrer Entwicklung, Leipzig, 1883) y El análisis de las sensaciones (Die Analyse der Empfindungen und das Verhältnis des Physischen zum Psychischen, Jena, 1886).^[7]​ Einstein siempre creyó que Mach había estado en el camino correcto para descubrir la relatividad en parte de sus trabajos de juventud, y que la única razón por la que no lo había hecho fue porque la época no fue la propicia.^[9]​ El artículo de 1905 de Einstein, titulado Zur Elektrodynamik bewegter Körper,^[1]​ cambió radicalmente la percepción del espacio y el tiempo que se tenía en ese entonces. En ese artículo Einstein introducía lo que ahora conocemos como teoría de la relatividad especial. Esta teoría se basaba en el principio de relatividad y en la constancia de la velocidad de la luz en cualquier sistema de referencia inercial. De ello Einstein dedujo las ecuaciones de Lorentz. También reescribió las relaciones del momento y de la energía cinética para que éstas también se mantuvieran invariantes.

La teoría permitió establecer la equivalencia entre masa y energía y una nueva definición del espacio-tiempo. De ella se derivaron predicciones y surgieron curiosidades. Como ejemplos, un observador atribuye a un cuerpo en movimiento una longitud más corta que la que tiene el cuerpo en reposo y la duración de los eventos que afecten al cuerpo en movimiento son más largos con respecto al mismo evento medido por un observador en el sistema de referencia del cuerpo en reposo.

En 1912, Wilhelm Wien, premio Nobel de Física de 1911, propuso a Lorentz y a Einstein para este galardón por la teoría de la relatividad, expresando

Aunque Lorentz debe ser considerado como el primero en encontrar la expresión matemática del principio de la relatividad, Einstein consiguió reducirlo desde un principio simple. Debemos pues considerar el mérito de los dos investigadores como comparable.

Wilhelm Wien^[10]​

Einstein no recibió el premio Nobel por la relatividad especial pues el comité, en principio, no otorgaba el premio a teorías puras. El Nobel no llegó hasta 1921, y fue por su trabajo sobre el efecto fotoeléctrico.^[11]​

Postulados

Velocidad de la luz desde la Tierra a la Luna, situada a más de 380.000 km.

• Primer postulado. Principio especial de relatividad: Las leyes de la física son las mismas en todos los sistemas de referencia inerciales. En otras palabras, no existe un sistema inercial de referencia privilegiado, que se pueda considerar como absoluto.


• Segundo postulado. Invariancia de c: La velocidad de la luz en el vacío es una constante universal, c, que es independiente del movimiento de la fuente de luz.^[12]​

La fuerza del argumento de Einstein está en la forma en que se deducen de ella resultados sorprendentes y plausibles a partir de dos simples hipótesis y cómo estas predicciones las confirmaron las observaciones experimentales.^[5]​ Matemáticamente hablando, en ambos postulados, tomados en conjunto, implicaban que cualquier ley física debía ser invariante respecto a una transformación de Lorentz. Es decir, que en todos los sistemas inerciales la forma matemática de las ecuaciones debía ser forminvariante de Lorentz.

Cuando se aplican estos dos principios a las ecuaciones de Maxwell se ve que éstas sólo son invariantes bajo las transformaciones de Lorentz, lo que implica que el intervalo de tiempo entre dos sucesos o la distancia entre dos puntos deben ser relativos al observador. Es decir, no todos los observadores medirán el mismo intervalo de tiempo entre dos sucesos o la misma longitud para un mismo objeto. Ese carácter no absoluto, sino relativo del espacio y el tiempo, que es una consecuencia de requerir que las medidas tomadas por diferentes observadores dejen invariantes las ecuaciones de Maxwell es la fuente de todos los resultados sorprendentes de la teoría de la relatividad. Cuando se examinan las leyes de Newton y otras leyes del movimiento de la mecánica clásica se aprecia que estas deben ser modificadas para ser también invariantes según las mismas transformaciones que las ecuaciones de Maxwell.

Principio de relatividad

Henri Poincaré, matemático francés, sugirió a finales del siglo XIX que el principio de relatividad establecido desde Galileo (la invariancia galileana) se mantiene para todas las leyes de la naturaleza. Joseph Larmor y Hendrik Lorentz descubrieron que las ecuaciones de Maxwell, la piedra angular del electromagnetismo, eran invariantes solo por una variación en el tiempo y una cierta unidad longitudinal, lo que produjo mucha confusión en los físicos, que en aquel tiempo estaban tratando de argumentar las bases de la teoría del éter, la hipotética substancia sutil que llenaba el vacío y en la que se transmitía la luz. El problema es que este éter era incompatible con el principio de relatividad.

En su publicación de 1905 en electrodinámica, Albert Einstein explicó que, con las transformaciones hechas por Lorentz, este principio se mantenía perfectamente invariable. La contribución de Einstein fue el elevar este axioma a principio y proponer las transformadas de Lorentz como primer principio. Además descartó la noción de tiempo absoluto y requirió que la velocidad de la luz en el vacío sea la misma para todos los observadores, sin importar si éstos se movían o no. Esto era fundamental para las ecuaciones de Maxwell, ya que éstas necesitan de una invarianza general de la velocidad de la luz en el vacío.

Covariancia de Lorentz

La teoría de la relatividad especial además busca formular todas las leyes físicas de forma que tengan validez para todos los observadores inerciales. Por lo que cualquier ley física debería tener una forma matemática invariante bajo unas transformaciones de Lorentz.

Transformaciones de Lorentz

Diferentes sistemas de referencia para un mismo fenómeno.

Como se ha mencionado, los físicos de la época habían encontrado una inconsistencia entre la completa descripción del electromagnetismo realizada por Maxwell y la mecánica clásica. Para ellos, la luz era una onda electromagnética transversal que se movía por un sistema de referencia privilegiado, al cual lo denominaban éter.

Hendrik Antoon Lorentz trabajó en resolver este problema y fue desarrollando unas transformaciones para las cuales las ecuaciones de Maxwell quedaban invariantes y sin necesidad de utilizar ese hipotético éter. La propuesta de Lorentz de 1899, conocida como la Teoría electrónica de Lorentz, no excluía —sin embargo— al éter. En la misma, Lorentz proponía que la interacción eléctrica entre dos cuerpos cargados se realizaba por medio de unos corpúsculos a los que llamaba electrones y que se encontraban adheridos a la masa en cada uno de los cuerpos. Estos electrones interactuaban entre sí mediante el éter, el cual era contraído por los electrones acorde a transformaciones específicas, mientras estos se encontraban en movimiento relativo al mismo. Estas transformaciones se las conoce ahora como transformaciones de Lorentz. La formulación actual fue trabajo de Poincaré, el cual las presentó de una manera más consistente en 1905.

Se tiene un sistema S de coordenadas (x,y,z,t){displaystyle (x,y,z,t),} y un sistema S' de coordenadas (x′,y′,z′,t′){displaystyle (x',y',z',t'),}, de aquí las ecuaciones que describen la transformación de un sistema a otro son:

t′=γ(t−vxc2),x′=γ(x−vt),y′=y,z′=z{displaystyle t'=gamma left(t-{frac {vx}{c^{2}}}right),qquad x'=gamma (x-vt),qquad y'=y,qquad z'=z,}

donde

γ=11−v2/c2{displaystyle gamma ={frac {1}{sqrt {1-v^{2}/c^{2}}}}}

es el llamado factor de Lorentz y c{displaystyle c,} es la velocidad de la luz en el vacío.

Contrario a nuestro conocimiento actual, en aquel momento esto era una completa revolución, debido a que se planteaba una ecuación para transformar al tiempo, cosa que para la época era imposible. En la mecánica clásica, el tiempo era un invariante. Y para que las mismas leyes se puedan aplicar en cualquier sistema de referencia se obtiene otro tipo de invariante a grandes velocidades (ahora llamadas relativistas), la velocidad de la luz.

Simultaneidad

Directamente de los postulados expuestos arriba, y por supuesto de las transformaciones de Lorentz, se deduce el hecho de que no se puede decir con sentido absoluto que dos acontecimientos hayan ocurrido al mismo tiempo en diferentes lugares. Si dos sucesos ocurren simultáneamente en lugares separados espacialmente desde el punto de vista de un observador, cualquier otro observador inercial que se mueva respecto al primero los presencia en instantes distintos.^[13]​

Matemáticamente, esto puede comprobarse en la primera ecuación de las transformaciones de Lorentz:

Δt′=γ(Δt−vΔxc2){displaystyle Delta t'=gamma left(Delta t-{frac {vDelta x}{c^{2}}}right)}

Dos eventos simultáneos verifican Δt=0{displaystyle displaystyle Delta t=0}, pero si sucedieron en lugares distintos (con Δx≠0{displaystyle Delta xneq 0}), otro observador con movimiento relativo obtiene Δt′≠0{displaystyle Delta t'neq 0}. Sólo en el caso Δt=0{displaystyle displaystyle Delta t=0} y Δx=0{displaystyle displaystyle Delta x=0} (sucesos simultáneos en el mismo punto) no ocurre esto.

El concepto de simultaneidad puede definirse como sigue. Dados dos eventos puntuales E₁ y E₂, que ocurre respectivamente en instantes de tiempo t₁ y t₂, y en puntos del espacio P₁ = (x₁, y₁, z₁) y P₂ = (x₂, y₂, z₂), todas las teorías físicas admiten que estos sólo pueden darse una, de tres posibilidades mutuamente excluyentes:^[14]​

1. Es posible para un observador estar presente en el evento E₁ y luego estar en el evento E₂, y en ese caso se afirma que E₁ es un evento anterior a E₂. Además si eso sucede no puede existir otro observador que verifique 2.


2. Es posible para un observador estar presente en el evento E₂ y luego estar en el evento E₁, y en ese caso se afirma que E₁ es un evento posterior a E₂. Además si eso sucede no puede existir otro observador que verifique 1.


3. Es imposible para algún observador puntual, estar presente simultáneamente en los eventos E₁ y E₂.

Dado un evento cualquiera, el conjunto de eventos puede dividirse según esas tres categorías anteriores. Es decir, todas las teorías físicas permiten fijado un evento, clasificar a los demás eventos: en (1) pasado, (2) futuro y (3) resto de eventos (ni pasados ni futuros). En mecánica clásica esta última categoría está formada por los sucesos llamados simultáneos, y en mecánica relativista eventos no relacionados causalmente con el primer evento. Sin embargo, la mecánica clásica y la mecánica relativista difieren en el modo concreto en que esa división entre pasado, futuro y otros puede hacerse y en si dicho carácter es absoluto o relativo de dicha partición.

Dilatación del tiempo y contracción de la longitud

Como se dijo previamente, el tiempo en esta teoría deja de ser absoluto como se proponía en la mecánica clásica. O sea, el tiempo para todos los observadores del fenómeno deja de ser el mismo. Si tenemos un observador inmóvil haciendo una medición del tiempo de un acontecimiento y otro que se mueva a velocidades relativistas, los dos relojes no tendrán la misma medición de tiempo.

Mediante la transformación de Lorentz nuevamente llegamos a comprobar esto. Se coloca un reloj ligado al sistema S y otro al S', lo que nos indica que x=0{displaystyle x=0}. Se tiene las transformaciones y sus inversas en términos de la diferencia de coordenadas:

Δt′=γ(Δt−vΔxc2){displaystyle Delta t'=gamma left(Delta t-{frac {vDelta x}{c^{2}}}right)}

Δx′=γ(Δx−vΔt){displaystyle Delta x'=gamma (Delta x-vDelta t),}

y

Δt=γ(Δt′+vΔx′c2){displaystyle Delta t=gamma left(Delta t'+{frac {vDelta x'}{c^{2}}}right)}

Δx=γ(Δx′+vΔt′){displaystyle Delta x=gamma (Delta x'+vDelta t'),}

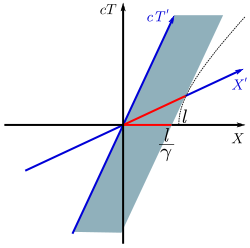
Gráfico que explica la contracción de Lorentz.

Si despejamos las primeras ecuaciones obtenemos

Δt′=γΔt({displaystyle Delta t'=gamma Delta tqquad (,} para sucesos que satisfagan Δx=0){displaystyle Delta x=0),}

De lo que obtenemos que los eventos que se realicen en el sistema en movimiento S' serán más largos que los del S. La relación entre ambos es esa γ{displaystyle gamma }. Este fenómeno se lo conoce como dilación del tiempo.

Si se dice que el tiempo varía a velocidades relativistas, la longitud también lo hace. Un ejemplo sería si tenemos a dos observadores inicialmente inmóviles, éstos miden un vehículo en el cual solo uno de ellos "viajará" a grandes velocidades, ambos obtendrán el mismo resultado. Uno de ellos entra al vehículo y cuando adquiera la suficiente velocidad mide el vehículo obteniendo el resultado esperado, pero si el que esta inmóvil lo vuelve a medir, obtendrá un valor menor. Esto se debe a que la longitud también se contrae.

Volviendo a las ecuaciones de Lorentz, despejando ahora a x y condicionando a  Δt′=0{displaystyle Delta t'=0} se obtiene:

Δx′=Δxγ{displaystyle Delta x'={frac {Delta x}{gamma }}qquad ,}

de lo cual podemos ver que existirá una disminución debido al cociente. Estos efectos solo pueden verse a grandes velocidades, por lo que en nuestra vida cotidiana las conclusiones obtenidas a partir de estos cálculos no tienen mucho sentido.

Un buen ejemplo de estas contracciones y dilataciones fue propuesto por Einstein en su paradoja de los gemelos, y verificado experimentalmente por la anomalía en el tiempo de vida de los muones, producidos por los rayos cósmicos.^[15]​

Cantidades relativistas

El pájaro se mueve con velocidad v respecto al sistema S. Sin embargo, desde el punto de vista del piloto del avión, el pájaro se aleja de él a una velocidad v′ mayor, dada por las fórmulas del texto.

Composición de velocidades

La composición de velocidades es el cambio en la velocidad de un cuerpo al ser medida en diferentes sistemas de referencia inerciales. En la física pre-relativista se calculaba mediante

v′=v+u{displaystyle v'=v+u} ,

donde v′ es la velocidad del cuerpo con respecto al sistema S′, u la velocidad con la que este sistema se aleja del sistema "en reposo" S, y v es la velocidad del cuerpo medida en S.

Sin embargo, debido a las modificaciones del espacio y el tiempo, esta relación no es válida en Relatividad Especial. Mediante las transformadas de Lorentz puede obtenerse la fórmula correcta:

v′=v+u1+u⋅vc2{displaystyle v'={frac {v+u}{1+{frac {ucdot v}{c^{2}}}}}}

Al observar con cuidado esta fórmula se nota que si tomamos para el cuerpo una velocidad en el sistema S igual a la de la luz (el caso de un fotón, por ejemplo), su velocidad en S′ sigue siendo v′=c, como se espera debido al segundo postulado. Además, si las velocidades son muy pequeñas en comparación con la luz, se obtiene que esta fórmula se aproxima a la anterior dada por Galileo.

Masa, momento y energía relativista

El concepto de masa en la teoría de la relatividad especial tiene dos bifurcaciones: la masa invariante y la masa relativista aparente. La masa relativista aparente es la masa aparente que va a depender del observador y se puede incrementar dependiendo de su velocidad, mientras que la invariante es independiente del observador e invariante.

Matemáticamente tenemos que:  M=γm{displaystyle M=gamma m} donde  M{displaystyle M} es la masa relativista aparente,  m{displaystyle m} es la invariante y  γ{displaystyle gamma } es el factor de Lorentz. Notemos que si la velocidad relativa del factor de Lorentz es muy baja, la masa relativa tiene el mismo valor que la masa invariante pero si ésta es comparable con la velocidad de la luz existe una variación entre ambas. Conforme la velocidad se vaya aproximando a la velocidad de la luz, la masa relativista tenderá a infinito.

Cantidad de movimiento

Al existir una variación en la masa relativista aparente, la cantidad de movimiento de un cuerpo también debe ser redefinida. Según Newton, la cantidad de movimiento está definida por  p=mv{displaystyle p=mv} donde  m{displaystyle m} era la masa del cuerpo. Como esta masa ya no es invariante, nuestra nueva "cantidad de movimiento relativista" tiene el factor de Lorentz incluido así:

 p=γmv=Mv{displaystyle p=gamma mv=Mv}

Sus consecuencias las veremos con más detenimiento en la sección posterior de fuerza.

Equivalencia de masa y energía

Equivalencia entre masa y energía.

La relatividad especial postula una ecuación para la energía, la cual inexplicablemente llegó a ser la ecuación más famosa del planeta, E = mc². A esta ecuación también se la conoce como la equivalencia entre masa y energía. En la relatividad, la energía y el momento de una partícula están relacionados mediante la ecuación:

E2−p2c2=m2c4{displaystyle E^{2}-p^{2}c^{2}=m^{2}c^{4}}

Esta relación de energía-momento formulada en la relatividad nos permite observar la independencia del observador tanto de la energía como de la cantidad de momento. Para velocidades no relativistas, la energía puede ser aproximada mediante una expansión de una serie de Taylor así

E=mc21−(v2/c2)≈mc2+12mv2{displaystyle E={cfrac {mc^{2}}{sqrt {1-(v^{2}/c^{2})}}}approx mc^{2}+{frac {1}{2}}mv^{2}}

encontrando así la energía cinética de la mecánica de Newton. Lo que nos indica que esa

mecánica no era más que un caso particular de la actual relatividad. El primer término de esta aproximación es lo que se conoce como la energía en reposo (energía potencial), ésta es la cantidad de energía que puede medir un observador en reposo de acuerdo con lo postulado por Einstein. Esta energía en reposo no causaba conflicto con lo establecido anteriormente por Newton, porque ésta es constante y además persiste la energía en movimiento. Einstein lo describió de esta manera:

Bajo esta teoría, la masa ya no es una magnitud inalterable pero sí una magnitud dependiente de (y asimismo, idéntica con) la cantidad de energía.^[16]​

Albert Einstein

Fuerza

En mecánica newtoniana la fuerza no relativista puede obtenerse simplemente como la derivada temporal del momento lineal:

F=dpdt{displaystyle mathbf {F} ={frac {dmathbf {p} }{dt}}},

Pero contrariamente postula la mecánica newtoniana, aquí el momento no es simplemente la masa en reposo por la velocidad. Por lo que la ecuación F=ma{displaystyle mathbf {F} =mmathbf {a} } ya no es válida en relatividad. Si introducimos la definición correcta del momento lineal, usando la masa aparente relativista entonces obtenemos la expresión relativista correcta:

F=d(Mv)dt=dMdtv+Mdvdt=mdγdtv+γmdvdt{displaystyle mathbf {F} ={frac {d(Mmathbf {v} )}{dt}}={frac {dM}{dt}}mathbf {v} +M{frac {dmathbf {v} }{dt}}=m{frac {dgamma }{dt}}mathbf {v} +gamma m{frac {dmathbf {v} }{dt}}}

donde  M=γm{displaystyle M=gamma m} es la masa relativista aparente. Calculando la fuerza anterior se observa el hecho que la fuerza podría no tener necesariamente la dirección de la aceleración, como se deduce desarrollando la ecuación anterior:

F=γma+γ3mv⋅ac2v{displaystyle mathbf {F} =gamma mmathbf {a} +gamma ^{3}m{frac {mathbf {v} cdot mathbf {a} }{c^{2}}}mathbf {v} }

Introduciendo las aceleraciones normal y tangencial:

F=γ3mate^t+γmane^n⇒[FtFn]=m[γ300γ][atan]{displaystyle mathbf {F} =gamma ^{3}ma_{t}mathbf {{hat {e}}_{t}} +gamma ma_{n}mathbf {{hat {e}}_{n}} quad Rightarrow quad {begin{bmatrix}F_{t}\F_{n}end{bmatrix}}=m{begin{bmatrix}gamma ^{3}&0\0&gamma end{bmatrix}}{begin{bmatrix}a_{t}\a_{n}end{bmatrix}}}

Existen dos casos particulares de movimiento de una partícula donde la fuerza es siempre paralela a la aceleración, que son el movimiento rectilíneo uniformemente acelerado y el movimiento circular uniforme; en el primer caso el factor de proporcionalidad es γ3m{displaystyle gamma ^{3}m,} y el en segundo γm{displaystyle gamma m,}

La geometría del espacio tiempo

La relatividad especial usa tensores y cuadrivectores para representar un espacio pseudo-euclídeo. Este espacio, sin embargo, es similar al espacio euclídeo tridimensional en muchos aspectos y es relativamente fácil trabajar en él. El tensor métrico que da la distancia elemental (ds) en un espacio euclídeo se define como:

ds2=dx12+dx22+dx32{displaystyle {text{d}}s^{2}={text{d}}x_{1}^{2}+{text{d}}x_{2}^{2}+{text{d}}x_{3}^{2}}

donde (dx1,dx2,dx3){displaystyle (dx_{1},dx_{2},dx_{3}),} son diferenciales de las tres coordenadas cartesianas espaciales. En la geometría de la relatividad especial, se añade una cuarta dimensión imaginaria dada por el producto ict, donde t es el tiempo, c la velocidad de la luz e i la unidad imaginaria: quedando el intervalo relativista, en forma diferencial, como:

ds2=dx12+dx22+dx32+(icdt)2{displaystyle {text{d}}s^{2}={text{d}}x_{1}^{2}+{text{d}}x_{2}^{2}+{text{d}}x_{3}^{2}+(ic{text{d}}t)^{2}}

El factor imaginario se introduce para mostrar el carácter pseudoeuclídeo de la geometría espacio-tiemporal. Si se reducen las dimensiones espaciales a 2, se puede hacer una representación física en un espacio tridimensional,

ds2=dx12+dx22−c2dt2{displaystyle {text{d}}s^{2}={text{d}}x_{1}^{2}+{text{d}}x_{2}^{2}-c^{2}{text{d}}t^{2}}

Cono dual.

Se puede ver que las geodésicas con medida cero forman un cono dual definido por la ecuación

ds2=0=dx12+dx22−c2dt2{displaystyle {text{d}}s^{2}=0={text{d}}x_{1}^{2}+{text{d}}x_{2}^{2}-c^{2}{text{d}}t^{2}}

dx12+dx22=c2dt2{displaystyle {text{d}}x_{1}^{2}+{text{d}}x_{2}^{2}=c^{2}{text{d}}t^{2}}

La ecuación anterior es la de círculo con  r=cdt{displaystyle r=c{text{d}}t}. Si se extiende lo anterior a las tres dimensiones espaciales, las geodésicas nulas son esferas concéntricas, con radio = distancia = c por tiempo.

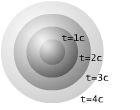
Esferas concéntricas.

ds2=0=dx12+dx22+dx32−c2dt2{displaystyle {text{d}}s^{2}=0={text{d}}x_{1}^{2}+{text{d}}x_{2}^{2}+{text{d}}x_{3}^{2}-c^{2}{text{d}}t^{2}}

dx12+dx22+dx32=c2dt2{displaystyle {text{d}}x_{1}^{2}+{text{d}}x_{2}^{2}+{text{d}}x_{3}^{2}=c^{2}{text{d}}t^{2}}

Este doble cono de distancias nulas representa el horizonte de visión de un punto en el espacio. Esto es, cuando se mira a las estrellas y se dice: La estrella de la que estoy recibiendo luz tiene X años, se está viendo a través de esa línea de visión: una geodésica de distancia nula. Se está viendo un suceso a d=x12+x22+x32{displaystyle d={sqrt {x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}}} metros, y  d/c{displaystyle d/c} segundos en el pasado. Por esta razón, el doble cono es también conocido como cono de luz (El punto inferior de la izquierda del diagrama inferior representa la estrella, el origen representa el observador y la línea representa la geodésica nula, el "horizonte de visión" o cono de luz). Es importante notar que sólo los puntos interiores al cono de luz de un evento pueden estar en relación causal con ese evento.

Causalidad física

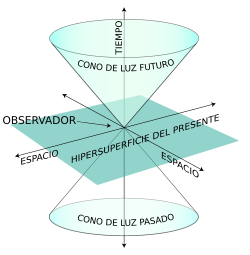
Un evento en un cono de luz temporal.

Previo a esta teoría, el concepto de causalidad estaba determinado: para una causa existe un efecto. Anteriormente, gracias a los postulados de Laplace, se creía que para todo acontecimiento se debía obtener un resultado que podía predecirse. La revolución en este concepto es que se "crea" un cono de luz de posibilidades (Véase gráfico adjunto).

Se observa este cono de luz y ahora un acontecimiento en el cono de luz del pasado no necesariamente nos conduce a un solo efecto en el cono de luz futuro. Desligando así la causa y el efecto. El observador que se sitúa en el vértice del cono ya no puede indicar qué causa del cono del pasado provocará el efecto en el cono del futuro.

Imposibilidad de movimientos más rápidos que la luz

Asumiendo el principio de causalidad e ingnorando ciertas posibilidades relacionadas con el movimiento superlumínico, obtenemos que ninguna partícula de masa positiva en reposo puede viajar más rápido que la luz. En particular, la relación entre la energía cinética K necesaria para acelerar rectilíneamente una partícula desde el reposo hasta una cierta velocidad v viene expresada por la ecuación:

v=c 1−m2c4(mc2+K)2{displaystyle v=c {sqrt {1-{frac {m^{2}c^{4}}{(mc^{2}+K)^{2}}}}}}

Aquí puede verse claramente que para cualquier valor finito de K se cumplirá que v < c. Otra manera de ver esta imposibilidad es usar el principio de causalidad, y aplicarlo al movimiento más rápido que el de la luz. Imagínese un cuerpo que experimenta una fuerza durante una cantidad infinita de tiempo. Tenemos entonces que para un movimiento rectilíneo:

F=dpdt=d(γmv)dt=mγ3a=m a[1−(v2/c2)]3/2{displaystyle F={frac {{text{d}}p}{{text{d}}t}}={frac {{text{d}}(gamma mv)}{{text{d}}t}}=mgamma ^{3}a={frac {m a}{[1-(v^{2}/c^{2})]^{3/2}}}}

De la expresión anterior se deduce que la "inercia efectiva", entendida como la resistencia que opone el cuerpo a ser acelerado F / a, irá aumentando indefinidamente a medida que v se acerca a c.

Por otra parte, esta conclusión depende críticamente de la asunción de causalidad. Así en mecánica cuántica esta asunción no se considera, por lo que algunas partículas virtuales no están sujetas a esa restricción. Además existen propuestas teóricas que postulan la existencia de partículas hipotéticas que podrían viajar más rápido que la luz, los taquiones, naturalmente en esas teorías no se asume el principio de causalidad en la forma planteada aquí.

Formulación matemática de la relatividad especial

La relatividad especial a pesar de poder ser descrita con facilidad por medio de la mecánica clásica y ser de fácil entendimiento, tiene una compleja matemática de por medio. Aquí se describe a la relatividad especial en la forma de la covariancia de Lorentz. La posición de un evento en el espacio-tiempo está dado por un vector contravariante cuatridimensional, sus componentes son:

xν=(t,x,y,z){displaystyle x^{nu }=left(t,x,y,zright)}

esto es que x0=t{displaystyle x^{0}=t}, x1=x{displaystyle x^{1}=x}, x2=y{displaystyle x^{2}=y} y x3=z{displaystyle x^{3}=z}. Los superíndices de esta sección describen contravarianza y no exponente a menos que sea un cuadrado o se diga lo contrario. Los superíndices son índices covariantes que tienen un rango de cero a tres como un gradiente del espacio tiempo del campo φ:

∂0ϕ=∂ϕ∂t,∂1ϕ=∂ϕ∂x,∂2ϕ=∂ϕ∂y,∂3ϕ=∂ϕ∂z.{displaystyle partial _{0}phi ={frac {partial phi }{partial t}},quad partial _{1}phi ={frac {partial phi }{partial x}},quad partial _{2}phi ={frac {partial phi }{partial y}},quad partial _{3}phi ={frac {partial phi }{partial z}}.}

Métrica y transformación de coordenadas

Habiendo reconocido la naturaleza cuatridimensional del espacio-tiempo, se puede empezar a emplear la métrica de Minkowski, η, dada en los componentes (válidos para cualquier sistema de referencia) así:

ηαβ=(−c2000010000100001){displaystyle eta _{alpha beta }={begin{pmatrix}-c^{2}&0&0&0\0&1&0&0\0&0&1&0\0&0&0&1end{pmatrix}}}

Su inversa es:

ηαβ=(−1c2000010000100001){displaystyle eta ^{alpha beta }={begin{pmatrix}-{frac {1}{c^{2}}}&0&0&0\0&1&0&0\0&0&1&0\0&0&0&1end{pmatrix}}}

Luego se reconoce que las transformaciones coordenadas entre los sistemas de referencia inerciales están dadas por el tensor de transformación de Lorentz Λ. Para el caso especial de movimiento a través del eje x, se tiene:

Λνμ′=(γ−βγ/c00−βγcγ0000100001){displaystyle Lambda _{nu }^{mu '}={begin{pmatrix}gamma &-beta gamma /c&0&0\-beta gamma c&gamma &0&0\0&0&1&0\0&0&0&1end{pmatrix}}}

que es simplemente la matriz de un boost (como una rotación) entre las coordenadas x y t. Donde μ' indica la fila y ν la columna. También β y γ están definidos como:

β=vc,γ=11−β2{displaystyle beta ={frac {v}{c}},qquad gamma ={frac {1}{sqrt {1-beta ^{2}}}}}

Más generalmente, una transformación de un sistema inercial (ignorando la translación para simplificarlo) a otro debe satisfacer:

ηαβ=ημ′ν′Λαμ′Λβν′{displaystyle eta _{alpha beta }=eta _{mu 'nu '}Lambda _{alpha }^{mu '}Lambda _{beta }^{nu '}!}

donde hay un sumatorio implícita de μ′{displaystyle mu '!} y ν′{displaystyle nu '!} de cero a tres en el lado derecho, de acuerdo con el Convenio de sumación de Einstein. El grupo de Poincaré es el grupo más general de transformaciones que preservan la métrica de Minkowski y ésta es la simetría física subyacente a la relatividad especial.

Todas las propiedades físicas cuantitativas son dadas por tensores. Así para transformar de un sistema a otro, se usa la muy conocida ley de transformación tensorial

T[j1′,j2′,…jq′][i1′,i2′,…ip′]=Λi1′i1Λi2′i2…Λip′ipΛj1′j1Λj2′j2…Λjq′jqT[j1,j2,…jq][i1,i2,…ip]{displaystyle T_{left[j_{1}',j_{2}',dots j_{q}'right]}^{left[i_{1}',i_{2}',dots i_{p}'right]}=Lambda ^{i_{1}'}{}_{i_{1}}Lambda ^{i_{2}'}{}_{i_{2}}dots Lambda ^{i_{p}'}{}_{i_{p}}Lambda _{j_{1}'}{}^{j_{1}}Lambda _{j_{2}'}{}^{j_{2}}dots Lambda _{j_{q}'}{}^{j_{q}}T_{left[j_{1},j_{2},dots j_{q}right]}^{left[i_{1},i_{2},dots i_{p}right]}}

donde Λjk′jk{displaystyle Lambda _{j_{k}'}{}^{j_{k}}!} es la matriz inversa de Λjk′jk{displaystyle Lambda ^{j_{k}'}{}_{j_{k}}!}. Para observar como esto es útil, transformamos la posición de un evento de un sistema de coordenadas S a uno S', se calcula

(t′x′y′z′)=Λμ′νxν=(γ−βγ/c00−βγcγ0000100001)(txyz)=(γt−γβx/cγx−βγctyz){displaystyle {begin{pmatrix}t'\x'\y'\z'end{pmatrix}}=Lambda ^{mu '}{}_{nu }x^{nu }={begin{pmatrix}gamma &-beta gamma /c&0&0\-beta gamma c&gamma &0&0\0&0&1&0\0&0&0&1end{pmatrix}}{begin{pmatrix}t\x\y\zend{pmatrix}}={begin{pmatrix}gamma t-gamma beta x/c\gamma x-beta gamma ct\y\zend{pmatrix}}}

que son las transformaciones de Lorentz dadas anteriormente. Todas las transformaciones de tensores siguen la misma regla. El cuadrado de la diferencia de la longitud de la posición del vector dxμ{displaystyle dx^{mu }!} construido usando

dx2=ημνdxμdxν=−(c⋅dt)2+(dx)2+(dy)2+(dz)2{displaystyle mathbf {{text{d}}x} ^{2}=eta _{mu nu }{text{d}}x^{mu }{text{d}}x^{nu }=-(ccdot {text{d}}t)^{2}+({text{d}}x)^{2}+({text{d}}y)^{2}+({text{d}}z)^{2},}

es un invariante. Ser invariante significa que toma el mismo valor en todos los sistemas inerciales porque es un escalar (tensor de rango 0), y así Λ no aparece en esta transformación trivial. Se nota que cuando el elemento línea dx2{displaystyle mathbf {dx} ^{2}} es negativo dτ=−dx2/c{displaystyle {text{d}}tau ={sqrt {-mathbf {{text{d}}x} ^{2}}}/c} es el diferencial del tiempo propio, mientras que cuando dx2{displaystyle mathbf {{text{d}}x} ^{2}} es positivo, dx2{displaystyle {sqrt {mathbf {{text{d}}x} ^{2}}}} es el diferencial de la distancia propia.

El principal valor de expresar las ecuaciones de la física en forma tensorial es que éstas son luego manifestaciones invariantes bajo los grupos de Poincaré, así que no tenemos que hacer cálculos tediosos o especiales para confirmar ese hecho. También al construir tales ecuaciones encontramos usualmente que ecuaciones previas que no tienen relación, de hecho, están conectadas cercanamente al ser parte de la misma ecuación tensorial.

Cuadrivelocidad y cuadriaceleración

Ahora podemos definir igualmente la velocidad y la aceleración mediante simples leyes de transformación. La velocidad en el espacio-tiempo U^μ está dada por

Uμ=dxμdτ=(γγvxγvyγvz){displaystyle U^{mu }={frac {{text{d}}x^{mu }}{{text{d}}tau }}={begin{pmatrix}gamma \gamma v_{x}\gamma v_{y}\gamma v_{z}end{pmatrix}}}

Reconociendo esto, podemos convertir buscando una ley sobre las composiciones de velocidades en un simple estado acerca de transformaciones de velocidades de cuatro dimensiones de una partícula de un sistema a otro. U^μ también tiene una forma invariante:

U2=ηνμUνUμ=−c2.{displaystyle {mathbf {U} }^{2}=eta _{nu mu }U^{nu }U^{mu }=-c^{2}.}

Así la cuadrivelocidad tiene una magnitud de c. Esta es una expresión del hecho que no hay tal cosa como la coordenada en reposo en relatividad: al menos, si se está siempre moviéndose a través del tiempo. Para la cuadriaceleración, ésta viene dada por Aμ=dUμ/dτ{displaystyle A^{mu }={text{d}}{mathbf {U} ^{mu }}/{text{d}}tau }. Dado esto, diferenciando la ecuación para τ produce

2ημνAμUν=0.{displaystyle 2eta _{mu nu }A^{mu }U^{nu }=0.!}

así en relatividad, la aceleración y la velocidad en el espacio-tiempo son ortogonales.

Cuadrimomento

El momento lineal y la energía se combinan en un cuadrivector covariante:

Pν=m ηνμUμ=(−E/cpxpypz){displaystyle P_{nu }=m eta _{nu mu }U^{mu }={begin{pmatrix}-E/c\p_{x}\p_{y}\p_{z}end{pmatrix}}}

donde m es la masa invariante.

La magnitud invariante del cuadrimomento es:

P2=ημνPμPν=−(E/c)2+p2.{displaystyle mathbf {P} ^{2}=eta ^{mu nu }P_{mu }P_{nu }=-(E/c)^{2}+mathbf {p} ^{2}.}

Podemos trabajar con que este es un invariante por el argumento de que éste es primero un escalar, no interesa qué sistema de referencia se calcule y si la transformamos a un sistema donde el momento total sea cero.

P2=−(Ereposo/c)2=−(mc)2.{displaystyle mathbf {P} ^{2}=-(E_{text{reposo}}/c)^{2}=-(mc)^{2}.}

Se observa que la energía en reposo es un invariante independiente. Una energía en reposo se puede calcular para partículas y sistemas en movimiento, por traslación de un sistema en que el momento es cero. La energía en reposo está relacionada con la masa de acuerdo con la ecuación antes discutida:

Ereposo=mc2 ,{displaystyle E_{text{reposo}}=mc^{2} ,}

Nótese que la masa de un sistema de medida en su sistema de centro de momento (donde el momento total es cero) está dado por la energía total del sistema en ese marco de referencia. No debería ser igual a la suma de masas individuales del sistema medido en otros sistemas.

Cuadrifuerza

Al usar la tercera ley de Newton, ambas fuerzas deben estar definidas como la tasa de cambio del momentum respecto al mismo tiempo coordenado. Esto es, se requiere de las fuerzas definidas anteriormente. Desafortunadamente, no hay un tensor en cuatro dimensiones que contenga las componentes de un vector de fuerza en tres dimensiones entre sus componentes.

Si una partícula no está viajando a c, se puede transformar en una fuerza de tres dimensiones del sistema de referencia de la partícula en movimiento entre los observadores de este sistema. A éstos se los suele llamar fuerza de cuatro dimensiones. Es la tasa de cambio del anterior vector de cuatro dimensiones de energía momento con respecto al tiempo propio. La versión covariante de esta fuerza es:

Fν=dpνdτ=(−dE/dτdpx/dτdpy/dτdpz/dτ){displaystyle F_{nu }={frac {{text{d}}p_{nu }}{{text{d}}tau }}={begin{pmatrix}-{{text{d}}E}/{{text{d}}tau }\{{text{d}}p_{x}}/{{text{d}}tau }\{{text{d}}p_{y}}/{{text{d}}tau }\{{text{d}}p_{z}}/{{text{d}}tau }end{pmatrix}}}

donde τ{displaystyle tau ,} es el tiempo propio.

En el sistema en reposo del objeto, la componente del tiempo de esta fuerza es cero a menos que la masa invariante del objeto este cambiando, en ese caso la tasa de cambio es negativa y es c² veces. En general, se piensa que las componentes de la fuerza de cuatro dimensiones no son iguales a las componentes de la fuerza de tres porque ésta de tres está definida por la tasa de cambio del momento con respecto al tiempo coordenado, así dp/dt{displaystyle {text{d}}p/{text{d}}t}; mientras que la fuerza en cuatro dimensiones está definida por la tasa de cambio del momento respecto al tiempo propio, así dp/dτ{displaystyle {text{d}}p/{text{d}}tau }.

En un medio continuo, la densidad de fuerza en tres dimensiones combinada con la densidad de potencia forma un vector de cuatro dimensiones covariante. La parte espacial es el resultado de dividir la fuerza en pequeñas células (en el espacio tridimensional) por el volumen de la célula. El componente del tiempo es negativo de la potencia transferida a la célula dividida para el volumen de la célula.

Temas avanzados

Unificando el electromagnetismo

Investigaciones teóricas en el electromagnetismo clásico indicaron el camino para descubrir la propagación de onda. Las ecuaciones generalizando los efectos electromagnéticos encontraron que la velocidad de propagación finita de los campos E y B requiere comportamientos claros en partículas cargadas. El estudio general de cargas en movimiento forma un potencial de Liénard-Wiechert, que es un paso a través de la relatividad especial.

La transformación de Lorentz del campo eléctrico de una carga en movimiento por un observador en reposo en un sistema de referencia resulta en la aparición de un término matemático comúnmente llamado campo magnético. Al contrario, el campo magnético generado por las cargas en movimiento desaparece y se convierte en un campo electrostático en un sistema de referencia móvil. Las ecuaciones de Maxwell son entonces simplemente ajustes empíricos a los efectos de la relatividad especial en un modelo clásico del universo. Como los campos eléctricos y magnéticos son dependientes de los sistemas de referencia y así entrelazados, en el así llamado campo electromagnético. La relatividad especial provee las reglas de transformación de cómo los campos electromagnéticos en un sistema inercial aparecen en otro sistema inercial.

Electromagnetismo

Las ecuaciones de Maxwell en la forma tridimensional son de por sí consistentes con el contenido físico de la relatividad especial. Pero debemos reescribirlas para hacerlas invariantes.^[17]​ La densidad de carga ρ{displaystyle rho !} y la densidad de corriente [Jx,Jy,Jz]{displaystyle [J_{x},J_{y},J_{z}]!} son unificadas en el concepto de vector cuatridimensional:

Jμ=(ρcJxJyJz){displaystyle J^{mu }={begin{pmatrix}rho c\J_{x}\J_{y}\J_{z}end{pmatrix}}}

La ley de conservación de la carga se vuelve:

∂μJμ=0.{displaystyle partial _{mu }J^{mu }=0.!}

El campo eléctrico [Ex,Ey,Ez]{displaystyle [E_{x},E_{y},E_{z}]!} y la inducción magnética [Bx,By,Bz]{displaystyle [B_{x},B_{y},B_{z}]!} son ahora unificadas en un tensor de campo electromagnético (de rango 2, antisimétrico covariante):

Fμν=(0−Ex−Ey−EzEx0Bz−ByEy−Bz0BxEzBy−Bx0){displaystyle F_{mu nu }={begin{pmatrix}0&-E_{x}&-E_{y}&-E_{z}\E_{x}&0&B_{z}&-B_{y}\E_{y}&-B_{z}&0&B_{x}\E_{z}&B_{y}&-B_{x}&0end{pmatrix}}}

La densidad de la fuerza de Lorentz fμ{displaystyle f_{mu }!} ejercida en la materia por el campo electromagnético es:

fμ=FμνJν.{displaystyle f_{mu }=F_{mu nu }J^{nu }.!}

La ley de Faraday de inducción y la ley de Gauss para el magnetismo se combinan en la forma:

∂λFμν+∂μFνλ+∂νFλμ=0.{displaystyle partial _{lambda }F_{mu nu }+partial _{mu }F_{nu lambda }+partial _{nu }F_{lambda mu }=0.!}

A pesar de que se ven muchas ecuaciones, éstas se pueden reducir a solo cuatro ecuaciones independientes. Usando la antisimetría del campo electromagnético se puede reducir a la identidad o redundar en todas las ecuaciones excepto las que λ, μ, ν = 1,2,3 o 2,3,0 o 3,0,1 o 0,1,2.

Sistemas no inerciales y relatividad especial

Existe cierta confusión sobre los límites de la teoría especial de la relatividad. Por ejemplo, con frecuencia en textos de divulgación se repite que dentro de esta teoría sólo pueden tratarse sistemas de referencia inerciales, en los cuales la métrica toma la forma canónica. Sin embargo, como diversos autores se han encargado de demostrar la teoría puede tratar igualmente sistemas de referencia no inerciales.^[18]​

Obviamente el tratamiento de sistemas no inerciales en la teoría de la relatividad especial resulta más complicado que el de los sistemas inerciales.

Einstein y otros autores consideraron antes del desarrollo de la relatividad general casi exclusivamente sistemas de coordenadas relacionados por transformaciones de Lorentz, razón por la cual se piensa que esta teoría es sólo aplicable a sistemas inerciales.

Relatividad general

Actualmente se considera como relatividad general el estudio del espacio-tiempo deformado por campos gravitatorios, dejando el estudio de los sistemas de referencia acelerados en espacios planos dentro de la relatividad especial. Igualmente la relatividad general es una de las teorías más relevantes para la construcción de modelos cosmológicos sobre el origen del universo.

La teoría general de la relatividad fue introducida históricamente en conexión con el principio de equivalencia y el intento de explicar la identidad entre la masa inercial y la masa gravitatoria. En esta teoría se usaban explícitamente sistemas de coordenadas no relacionados entre sí por transformaciones de Lorentz o similares, con lo cual claramente en la resolución de muchos problemas se hacía patente el uso de sistemas de referencia no inerciales. Estos hechos condujeron a la confusión en muchos textos de divulgación de que los sistemas no inerciales requieren del desarrollo de la teoría general de la relatividad.

Tests de postulados de la relatividad especial

• 
  Experimento Michelson-Morley – arrastre del éter.


• Experimento Hamar – obstrucción del flujo del éter.


• 
  Experimento Trouton-Noble – torque en un condensador producido por el arrastre del éter.


• 
  Experimento Kennedy-Thorndike – contracción del tiempo.


• Experimento sobre las formas de emisión.


• Experimento de Ives–Stilwell

Véase también

Personas: Arthur Eddington | Albert Einstein | Hendrik Lorentz | Hermann Minkowski | Bernhard Riemann | Henri Poincaré

Relatividad: Teoría de la relatividad | Principio de relatividad | sistema de referencia | sistema de referencia inercial |E=mc² | Pruebas de la relatividad especial

Física: mecánica newtoniana | espacio-tiempo | velocidad de la luz | cosmología física | efecto Doppler | ecuaciones relativistas de Euler | éter (física) | taquión | teoría relativista de la gravitación

Matemáticas: espacio de Minkowski | cono de luz | grupo de Lorentz | grupo de Poincaré | geometría | tensor

Referencias

Bibliografía

• 
  Alemañ Berenguer, Rafael Andrés (2004). Relatividad para todos. ISBN 84-95495-43-0. 
  


• 
  Alemañ Berenguer, Rafael Andrés (2005). Física para todos. ISBN 84-95495-60-0. 
  


• 
  Bertrand Russell, El ABC de la relatividad, 1925.

Enlaces externos

• 
  Wikimedia Commons alberga una categoría multimedia sobre Teoría de la relatividad especial.


• 
  Wikiquote alberga frases célebres de o sobre Teoría de la relatividad especial.


• 
  Wikilibros alberga un libro o manual sobre Teoría de la Relatividad para torpes.


• 
  Wikcionario tiene definiciones y otra información sobre Relatividad Especial.

• 
  Artículos en Wikinoticias: Dos alemanes aseguran haber superado la velocidad de la luz
  


• Contenido sencillo sobre relatividad (en inglés)


• Einstein y la revolución científica del siglo XX


• Einstein y la teoría especial de la relatividad. La abolición del espacio y el tiempo absolutos


• Ejercicios sobre Relatividad Especial


• Notas sobre Relatividad Especial


• "On the Electrodynamics of Moving Bodies", el artículo de Einstein donde plantea la RE (Jun 1905)(traducción al inglés)


• Relatividad sin fórmulas


• 
  Vídeos de objetos vistos a velocidades cuasilumínicas (Universidad de Tübingen)


• Artículo "Realitividad para tontos"


• Artículo original de Einstein en español